练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知，点，，，在射线ON上，点，，，在射线OM上，，，，均为等边三角形，若，则的边长为______．

    【答案】

    【解析】

    根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3，以及A2B2=2B1A2，得出A3B3=4B1A2=8，A4B4=8B1A2=16，A5B5=16B1A2…进而得出答案．

    ∵△A1B1A2是等边三角形，

    ∴A1B1=A2B1．

    ∵∠MON=30°，OA2=4，

    ∴OA1=A1B1=2，

    ∴A2B1=2．

    ∵△A2B2A3、△A3B3A4是等边三角形，

    ∴A1B1∥A2B2∥A3B3，B1A2∥B2A3，

    ∴A2B2=2B1A2，B3A3=2B2A3，

    ∴A3B3=4B1A2=8，A4B4=8B1A2=16，A5B5=16B1A2=32，

    以此类推△AnBnAn+1的边长为2n．

    故答案为：2n．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点A，B是数轴上的两个点，点A表示的数为﹣2，点B在点A右侧，距离A点12个单位长度，动点P从点A出发，以每秒2个单位长度的速度沿数轴向右匀速运动，设运动时间为t（t＞0）秒．

    （1）填空：①数轴上点B表示的数为　 　；

    ②数轴上点P表示的数为　 　（用含t的代数式表示）．

    （2）设AP和PB的中点分别为点M，N，在点P的运动过程中，线段M N的长度是否发生变化？若变化，请说明理由；若不变，求出线段M N的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察如图图形，它是按一定规律排列的，根据图形所揭示的规律我们可以发现：第1个图形十字星与五角星的个数和为7，第2个图形十字星与五角星的个数和为10，第3个图形十字星与五角星的个数和为13，按照这样的规律．则第8个图形中，十字星与五角星的个数和为（　　）

    A. 25B. 27C. 28D. 31

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系中，直线y=-x-与x轴交于点A，与y轴交于点B，点C在x轴正半轴上，且OC=3AO，过点A作BC的平行线l．

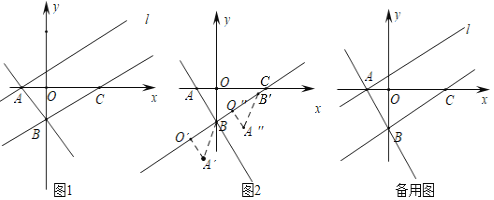
    （1）求直线BC的解析式；

    （2）作点A关于BC的对称点D，一动点P从C点出发按某一路径运动到直线l上的点M，再沿垂直BC的方向运动到直线BC上的点N，再沿某一路径运动到D点，求点P运动的最短路径的长以及此时点N的坐标；

    （3）如图2，将△AOB绕点B旋转，使得A′O′⊥BC，得到△A′O′B，将△A′O′B沿直线BC平移得到△A″O″B′，连接A″、B″、C，是否存在点A″，使得△A″B′C为等腰三角形？若存在，请直接写出点A″的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在2016年“双十一”期间，某快递公司计划租用甲、乙两种车辆快递货物，从货物量来计算：若租用两种车辆合运，10天可以完成任务；若单独租用乙种车辆，完成任务的天数是单独租用甲种车辆完成任务天数的2倍．

    (1)求甲、乙两种车辆单独完成任务分别需要多少天？

    (2)已知租用甲、乙两种车辆合运需租金65000元，甲种车辆每天的租金比乙种车辆每天的租金多1500元，试问：租甲和乙两种车辆、单独租甲种车辆、单独租乙种车辆这三种租车方案中，哪一种租金最少？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为D，BF平分∠ABC，交CD于点E，交AC于点F．若AB＝10，BC＝6，则CE的长为（　　）

    A. 3B. 4C. 5D. 6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图1，OM是∠AOB的平分线，点C在OM上，OC＝5，且点C到OA的距离为3．过点C作CD⊥OA，CE⊥OB，垂足分别为D、E，易得到结论：OD+OE等于多少；

    （1）把图1中的∠DCE绕点C旋转，当CD与OA不垂直时（如图2），上述结论是否成立？并说明理由；

    （2）把图1中的∠DCE绕点C旋转，当CD与OA的反向延长线相交于点D时：

    ①请在图3中画出图形；

    ②上述结论还成立吗？若成立，请给出证明；若不成立，请直接写出线段OD、OE之间的数量关系，不需证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=a（x﹣h）2+k（a，h，k为常数）在坐标平面上的图象通过（0，5）、（15，8）两点．若a＜0，0＜h＜10，则h之值可能为下列何值？（ ）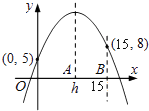

    A.5
    B.6
    C.7
    D.8

    查看答案和解析>>

    科目：初中数学 来源： 题型：

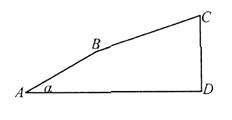
    【题目】如图，小刚从点 出发，沿着坡度为 的斜坡向上走了650米到达点 ，且 ．

    （1）则他上升的高度是 米 ；
    （2）然后又沿着坡度为 的斜坡向上走了1000米达到点 ．问小刚从 点到 点上升的高度 是多少米（结果保留根号）?

    查看答案和解析>>

    同步练习册答案