练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知二次函数y=a（x﹣h）2+k（a，h，k为常数）在坐标平面上的图象通过（0，5）、（15，8）两点．若a＜0，0＜h＜10，则h之值可能为下列何值？（ ）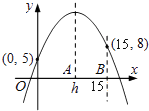

    A.5
    B.6
    C.7
    D.8

    【答案】D
    【解析】解：∵抛物线的对称轴为直线x=h，

    而（0，5）、（15，8）两点在抛物线上，

    ∴h﹣0＞15﹣h，解得h＞7.5．

    所以答案是：D

    【考点精析】利用二次函数图象以及系数a、b、c的关系对题目进行判断即可得到答案，需要熟知二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】电力公司为鼓励市民节约用电，采取按月用电量分段收费办法．若某户居民每月应交电费y（元）与用电量x（度）的函数图象是一条折线（如图所示），根据图象解下列问题：

    (1) 分别写出当0≤x≤100和x＞100时，y与x的函数关系式

    (2) 利用函数关系式，说明电力公司采取的收费标准

    (3) 若该用户某月用电62度，则应缴费多少元？若该用户某月缴费105元时，则该用户该月用了多少度电？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知，点，，，在射线ON上，点，，，在射线OM上，，，，均为等边三角形，若，则的边长为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等边△ABC中，AB＝2，N为AB上一点，且AN＝1，AD＝，∠BAC的平分线交BC于点D，M是AD上的动点，连接BM、MN，则BM+MN的最小值是（　　）

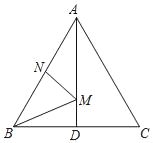
    A. B. 2C. 1D. 3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】平面直角坐标系xOy中，对于点P（a，b），若点P′的坐标为（a ，ka+b）（其中k为常数，且k≠0），则称点P′为点P的“k关联点”．

    （1）求点P（﹣2，3）的“2关联点”P′的坐标；
    （2）若a、b为正整数，点P的“k关联点”P′的坐标为（3，6），求出k及点P的坐标；
    （3）如图，点Q的坐标为（0，4 ），点A在函数y=﹣ （x＜0）的图象上运动，且点A是点B的“﹣ 关联点”，当线段BQ最短时，求B点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形中，，点在边上，点在边上，连接、、，下列说法：①若为中点，，则；②若为中点，，则；③若，，则点为中点，正确的有（ ）个

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】雾霾天气严重影响市民的生活质量．在去年寒假期间，某校八年级一班的综合实践小组同学对“雾霾天气的主要成因”随机调查了所在城市部分市民．并对调查结果进行了整理．绘制了如图不完整的统计图表．观察分析并回答下列问题．

    组别

    雾霾天气的主要成因

    百分比

    A

    工业污染

    45%

    B

    汽车尾气排放

    m

    C

    炉烟气排放

    15%

    D

    其他（滥砍滥伐等）

    n


    （1）本次被调查的市民共有多少人？
    （2）求m、n的值，并计算图2中区域B所对应的扇形圆心角的度数；
    （3）若该市有100万人口，请估计持有A、B两组主要成因的市民有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系中，点在轴正半轴，点在轴负半轴，连接，，

    （1）求点坐标

    （2）如图2，点是线段上一点，连接，以为直角边做等腰直角，，设点的横坐标为，求点的坐标（用含的代数式表示）

    （3）在（2）的条件下，如图3，在延长线上有一点，过点作的平行线，交轴于点，延长交于点，若，，求点的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（问题背景）

    （1）如图1的图形我们把它称为“8字形”，请说明∠A+∠B=∠C+∠D；

    （简单应用）

    （2）如图2， AP、CP分别平分∠BAD． ∠BCD，若∠ABC=46°，∠ADC=26°，求∠P的度数；

    （问题探究）

    （3）如图3，直线AP平分∠BAD的外角∠FAD，CP平分∠BCD的外角∠BCE，若∠ABC=36°，∠ADC=16°，请猜想∠P的度数，并说明理由．

    （拓展延伸）

    （4） ①在图4中，若设∠C=α，∠B=β，∠CAP=∠CAB，∠CDP=∠CDB，试问∠P与∠C、∠B之间的数量关系为： （用α、β表示∠P）；

    ②在图5中，AP平分∠BAD，CP平分∠BCD的外角∠BCE， 猜想∠P与∠B、∠D的关系，直接写出结论．

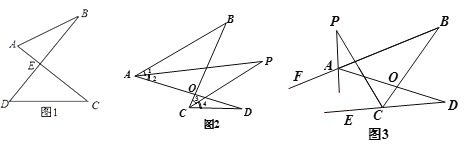
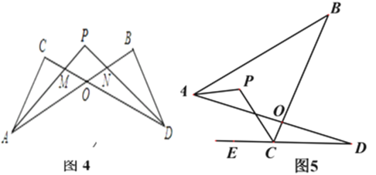
    查看答案和解析>>

    同步练习册答案