
【题目】如图1,在平面直角坐标系中,点![]() 在
在![]() 轴正半轴,点
轴正半轴,点![]() 在
在![]() 轴负半轴,连接
轴负半轴,连接![]() ,
,![]() ,
,![]()
(1)求点![]() 坐标
坐标
(2)如图2,点![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() ,以
,以![]() 为直角边做等腰直角
为直角边做等腰直角![]() ,
,![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示)
的代数式表示)
(3)在(2)的条件下,如图3,在![]() 延长线上有一点
延长线上有一点![]() ,过点
,过点![]() 作
作![]() 的平行线,交
的平行线,交![]() 轴于点
轴于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.



【答案】(1) 点B坐标为(-2,0),(2) 点E的坐标(2-m,m),(3)F点(1,3).
【解析】
(1)根据△AOB是等腰直角三角形可求出OA、OB长,即可得到B的坐标;
(2)作DM⊥OB,EN⊥X轴,垂足分别为M、N,易证△DOM≌△OEN,从而DM=ON,OM=EN,即可得到E点坐标;
(3)延长OD交HF延长线于P点,在y轴正半轴取R点使OR=OH,过F点作FM垂直于y轴,将AF=![]() GH转化为MF=GH=PR,再利用△RNP≌△FNM,△BOD≌△PFD,得PF=MR=OB=2, 设MF=m,MN=y,FN=2-y,则MA=m,OH=OR=4+m,用勾股定理和相似列方程组解出m即可解答.
GH转化为MF=GH=PR,再利用△RNP≌△FNM,△BOD≌△PFD,得PF=MR=OB=2, 设MF=m,MN=y,FN=2-y,则MA=m,OH=OR=4+m,用勾股定理和相似列方程组解出m即可解答.
解:(1)∵∠ABO=45°,
∴△AOB是等腰直角三角形,
∴2OB2=AB2,
∵AB=2![]()
∴OB=2,
∴点B坐标为(-2,0)
(2)作DM⊥OB,EN⊥X轴,垂足分别为M、N,
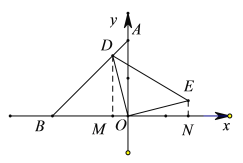
∵∠DOE=90°,
∴∠MDO=∠NOE,
在△DOM和△OEN中
 ,
,
∴△DOM≌△OEN(AAS)
∴DM=ON,OM=EN
∵△BMD、△BOA是等腰直角三角形,EN=OM=-m
∴ON=DM=2+m
∴点E的坐标(2+m,-m),
(3)延长OD交HF延长线于P点,在y轴正半轴取R点使OR=OH,过F点作FM垂直于y轴,
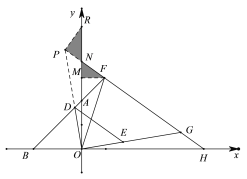
∵△DOE是等腰直角三角形,DE∥FH,
∴△POG是等腰直角三角形,
易证△POR≌△GOH,
∴PR=GH,∠PRN=∠GHO
∵MF⊥y轴,△AOB是等腰直角三角形,
∴△AMF是等腰直角三角形,∠GHO=∠NFM
∴AF=![]() MF,
MF,
又∵AF=![]() GH
GH
∴PR=GH=MF,
在△RNP和△FNM中
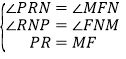 ,
,
△RNP≌△FNM(AAS)
∴PN=MN,FN=RN,
∴PF=MR
在△BOD和△PFD中,
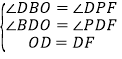
∴△BOD≌△PFD(AAS),
∴PF=OB=MR=2,
设MF=m,MN=y,FN=2-y,则MA=m,OH=OR=4+m
在Rt△MNF中,![]() ,
,
∴![]() ,
,
∵△MFN∽△OHN
∴![]() ,
,
∴![]() ,
,
联立解方程得m=1,
∴F点坐标为(1,3)


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=-![]() x-
x-![]() 与x轴交于点A,与y轴交于点B,点C在x轴正半轴上,且OC=3AO,过点A作BC的平行线l.
与x轴交于点A,与y轴交于点B,点C在x轴正半轴上,且OC=3AO,过点A作BC的平行线l.
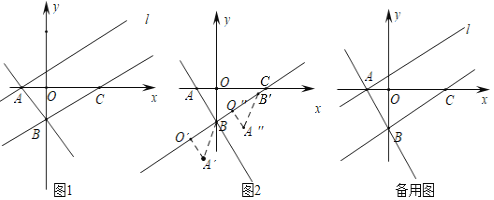
(1)求直线BC的解析式;
(2)作点A关于BC的对称点D,一动点P从C点出发按某一路径运动到直线l上的点M,再沿垂直BC的方向运动到直线BC上的点N,再沿某一路径运动到D点,求点P运动的最短路径的长以及此时点N的坐标;
(3)如图2,将△AOB绕点B旋转,使得A′O′⊥BC,得到△A′O′B,将△A′O′B沿直线BC平移得到△A″O″B′,连接A″、B″、C,是否存在点A″,使得△A″B′C为等腰三角形?若存在,请直接写出点A″的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x﹣h)2+k(a,h,k为常数)在坐标平面上的图象通过(0,5)、(15,8)两点.若a<0,0<h<10,则h之值可能为下列何值?( )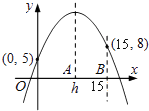
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】依据下列解方程![]() 的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据。
的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据。
解:原方程可变形为![]() ( )
( )
( ),得![]() ( )
( )
去括号,得![]()
( ),得![]() ( )
( )
合并同类项,得![]() (合并同类项法则)
(合并同类项法则)
( ),得![]() ( )
( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆运动(含P、Q两点),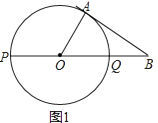
(1)当线段AB所在的直线与圆O相切时,求弧AQ的长(图1);
(2)若∠AOB=120°,求AB的长(图2);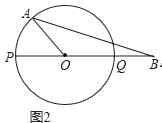
(3)如果线段AB与圆O有两个公共点A、M,当AO⊥PM于点N时,求tan∠MPQ的值(图3).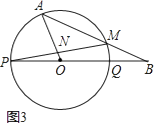
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小刚从点 ![]() 出发,沿着坡度为
出发,沿着坡度为 ![]() 的斜坡向上走了650米到达点
的斜坡向上走了650米到达点 ![]() ,且
,且 ![]() .
.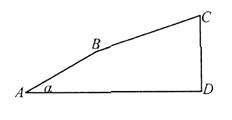
(1)则他上升的高度是 米 ;
(2)然后又沿着坡度为 ![]() 的斜坡向上走了1000米达到点
的斜坡向上走了1000米达到点 ![]() .问小刚从
.问小刚从 ![]() 点到
点到 ![]() 点上升的高度
点上升的高度 ![]() 是多少米(结果保留根号)?
是多少米(结果保留根号)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,矩形
中,矩形 ![]() 的边
的边 ![]() 在
在 ![]() 轴上,顶点
轴上,顶点 ![]() 在抛物线
在抛物线 ![]() 上,且抛物线交
上,且抛物线交 ![]() 轴于另一点
轴于另一点 ![]() .
.
(1)则 ![]() = ,
= , ![]() =;
=;
(2)已知 ![]() 为
为 ![]() 边上一个动点(不与
边上一个动点(不与 ![]() 、
、 ![]() 重合),连结
重合),连结 ![]() 交
交 ![]() 于点
于点 ![]() ,过点
,过点 ![]() 作
作 ![]() 轴的平行线分别交抛物线、直线
轴的平行线分别交抛物线、直线 ![]() 于
于 ![]() 、
、 ![]() .
.
①求线段 ![]() 的最大值,此时
的最大值,此时 ![]() 的面积为;
的面积为;
②若以点 ![]() 为圆心,
为圆心, ![]() 为半径作⊙O,试判断直线
为半径作⊙O,试判断直线 ![]() 与⊙O的能否相切,若能请求出
与⊙O的能否相切,若能请求出 ![]() 点坐标,若不能请说明理由.
点坐标,若不能请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根.华罗庚脱口而出:39.众人感觉十分惊奇,请华罗庚给大家解读其中的奥秘.
你知道怎样迅速准确的计算出结果吗?请你按下面的问题试一试:
①![]() ,又
,又![]() ,
,
![]() ,∴能确定59319的立方根是个两位数.
,∴能确定59319的立方根是个两位数.
②∵59319的个位数是9,又![]() ,∴能确定59319的立方根的个位数是9.
,∴能确定59319的立方根的个位数是9.
③如果划去59319后面的三位319得到数59,
而![]() ,则
,则![]() ,可得
,可得![]() ,
,
由此能确定59319的立方根的十位数是3
因此59319的立方根是39.
(1)现在换一个数195112,按这种方法求立方根,请完成下列填空.
①它的立方根是_______位数.
②它的立方根的个位数是_______.
③它的立方根的十位数是__________.
④195112的立方根是________.
(2)请直接填写结果:
①![]() ________.
________.
②![]() ________.
________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com