
【题目】雾霾天气严重影响市民的生活质量.在去年寒假期间,某校八年级一班的综合实践小组同学对“雾霾天气的主要成因”随机调查了所在城市部分市民.并对调查结果进行了整理.绘制了如图不完整的统计图表.观察分析并回答下列问题.
组别 | 雾霾天气的主要成因 | 百分比 |
A | 工业污染 | 45% |
B | 汽车尾气排放 | m |
C | 炉烟气排放 | 15% |
D | 其他(滥砍滥伐等) | n |
(1)本次被调查的市民共有多少人?
(2)求m、n的值,并计算图2中区域B所对应的扇形圆心角的度数;
(3)若该市有100万人口,请估计持有A、B两组主要成因的市民有多少人?
【答案】
(1)解:90÷45%=200(人).
所以本次被调查的市民共有200人;
(2)解:m= ![]() ×100%=30%;n=1﹣45%﹣30%﹣15%=10%;
×100%=30%;n=1﹣45%﹣30%﹣15%=10%;
图2中区域B所对应的扇形圆心角的度数=360°×30%=108°;
(3)解:100×(45%+30%)=75(万).
所以估计持有A、B两组主要成因的市民有75万人.
【解析】根据A的人数和所占的百分比,求出本次被调查的市民的人数。
(2)用B的人数除以总人数即可求出B的百分比;从而求出n的值。
(3)用该市的总人数乘以A、B两组主要成因的市民的百分比的和。即可求出结果。
【考点精析】掌握全面调查与抽样调查和扇形统计图是解答本题的根本,需要知道全面调查收集到的数据全面、准确,但一般花费多、耗时长,而且某些调查不宜用全面调查;抽样调查具有花费少、省时的特点,但抽取的样本是否具有代表性,直接关系到对总体估计的准确程度;能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况.


科目:初中数学 来源: 题型:
【题目】观察如图图形,它是按一定规律排列的,根据图形所揭示的规律我们可以发现:第1个图形十字星与五角星的个数和为7,第2个图形十字星与五角星的个数和为10,第3个图形十字星与五角星的个数和为13,按照这样的规律.则第8个图形中,十字星与五角星的个数和为( )

A. 25B. 27C. 28D. 31
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,OM是∠AOB的平分线,点C在OM上,OC=5,且点C到OA的距离为3.过点C作CD⊥OA,CE⊥OB,垂足分别为D、E,易得到结论:OD+OE等于多少;
(1)把图1中的∠DCE绕点C旋转,当CD与OA不垂直时(如图2),上述结论是否成立?并说明理由;
(2)把图1中的∠DCE绕点C旋转,当CD与OA的反向延长线相交于点D时:
①请在图3中画出图形;
②上述结论还成立吗?若成立,请给出证明;若不成立,请直接写出线段OD、OE之间的数量关系,不需证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x﹣h)2+k(a,h,k为常数)在坐标平面上的图象通过(0,5)、(15,8)两点.若a<0,0<h<10,则h之值可能为下列何值?( )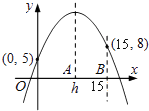
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】依据下列解方程![]() 的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据。
的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据。
解:原方程可变形为![]() ( )
( )
( ),得![]() ( )
( )
去括号,得![]()
( ),得![]() ( )
( )
合并同类项,得![]() (合并同类项法则)
(合并同类项法则)
( ),得![]() ( )
( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PQ为圆O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在圆O的上半圆运动(含P、Q两点),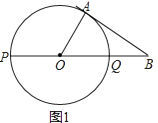
(1)当线段AB所在的直线与圆O相切时,求弧AQ的长(图1);
(2)若∠AOB=120°,求AB的长(图2);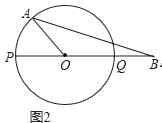
(3)如果线段AB与圆O有两个公共点A、M,当AO⊥PM于点N时,求tan∠MPQ的值(图3).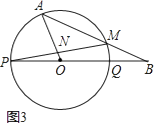
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小刚从点 ![]() 出发,沿着坡度为
出发,沿着坡度为 ![]() 的斜坡向上走了650米到达点
的斜坡向上走了650米到达点 ![]() ,且
,且 ![]() .
.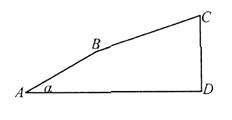
(1)则他上升的高度是 米 ;
(2)然后又沿着坡度为 ![]() 的斜坡向上走了1000米达到点
的斜坡向上走了1000米达到点 ![]() .问小刚从
.问小刚从 ![]() 点到
点到 ![]() 点上升的高度
点上升的高度 ![]() 是多少米(结果保留根号)?
是多少米(结果保留根号)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC 的角平分线与 BC 的垂直平分线交于点 D,DE⊥AB, DF⊥AC,垂足分别为 E,F.若 AB=10,AC=8,求 BE 长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com