
【题目】已知:如图1,OM是∠AOB的平分线,点C在OM上,OC=5,且点C到OA的距离为3.过点C作CD⊥OA,CE⊥OB,垂足分别为D、E,易得到结论:OD+OE等于多少;
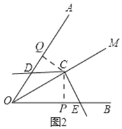
(1)把图1中的∠DCE绕点C旋转,当CD与OA不垂直时(如图2),上述结论是否成立?并说明理由;
(2)把图1中的∠DCE绕点C旋转,当CD与OA的反向延长线相交于点D时:
①请在图3中画出图形;
②上述结论还成立吗?若成立,请给出证明;若不成立,请直接写出线段OD、OE之间的数量关系,不需证明.

【答案】OD+OE=8;(1)上述结论成立,理由见解析;(2)①补全图形如图3,见解析;②上述结论不成立,OE﹣OD=8,理由见解析.
【解析】
先利用勾股定理求出OD,再利用角平分线定理得出DE=CD,即可得出结论;
(1)先判断出∠DCQ=∠ECP,进而判断出△CQD≌△CPE,得出DQ=PE,即可得出结论;
(2)①依题意即可补全图形;②同(1)的方法即可得出结论.
∵CD⊥OA,
∴∠ODC=90°,
在Rt△ODC中,CD=3,OC=5,
∴OD=![]() =4,
=4,
∵点C是∠AOB的平分线上的点,
∴DE=CD=3,
同理,OE=4,
∴OD+OE=4+4=8,
故答案为8;
(1)上述结论成立,理由:如图2,过点C作CQ⊥OA于Q,CP⊥OB于P,
∴∠OQC=∠EPC=90°,
∴∠AOB+∠POQ=180°,
由旋转知,∠AOB+∠DOE=180°,
∴∠POQ=∠DOE,
∴∠DCQ=∠ECP,
∵点C是∠AOB的平分线上,且CQ⊥OA,CP⊥OB,
∴CQ=CP,
∵∠OQC=∠EPC=90°,
∴△CQD≌△CPE(ASA),
∴DQ=PE,
∵OD=OQ﹣DQ,OE=OP+PE,
∴OD+OE=OQ﹣DQ+OP+PE=OQ+OP=8;
(2)①补全图形如图3
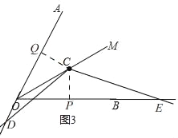
②上述结论不成立,OE﹣OD=8,
理由:过点C作CQ⊥OA于Q,CP⊥OB于P,
∴∠OQC=∠EPC=90°,
∴∠AOB+∠POQ=180°,
由旋转知,∠AOB+∠DOE=180°,
∴∠POQ=∠DOE,
∴∠DCQ=∠ECP,
∵点C是∠AOB的平分线上,且CQ⊥OA,CP⊥OB,
∴CQ=CP,
∵∠OQC=∠EPC=90°,
∴△CQD≌△CPE(ASA),
∴DQ=PE,
∵OD=DQ﹣OQ,OE=OP+PE,
∴OE﹣OD=OP+PE﹣(DQ﹣OQ)=OP+PE﹣DQ+OQ=OP+OQ=8.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=kx+b(k≠0)与x轴、y轴分别交于A、B两点,与直线l2:y=3x交于点C,其中点C的坐标为(![]() ,c),点B的坐标为(0,3).
,c),点B的坐标为(0,3).
(1)求点C的坐标;
(2)求直线l1的表达式;
(3)在x轴上有一点D(3,0),求△BCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(x-2)(x-3)=m有实数根x1 , x2 , 且x1![]() x2有下列结论:①x1=2,x2=3;②m>
x2有下列结论:①x1=2,x2=3;②m> ![]() ;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中正确的结论是(填正确结论的序号)
;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中正确的结论是(填正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究活动)
(1)问题发现:如图①,直线AB∥CD,E是AB与AD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC.

请把下面的证明过程补充完整:
证明:过点E作EF∥AB,
∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC( )
∴∠C=∠CEF.( )
∵EF∥AB,∴∠B=∠BEF(同理),
∴∠B+∠C= (等量代换)
即∠B+∠C=∠BEC.
(2)拓展探究:如果点E运动到图②所示的位置,其他条件不变,试探究∠B、∠C、∠BEC的数量关系并证明;
(3)解决问题:如图③,AB∥DC,∠C=120°,∠AEC=80°,则∠A= .(直接写出结论,不用写计算过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
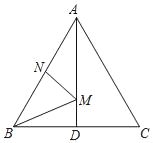
【题目】如图,在等边△ABC中,AB=2,N为AB上一点,且AN=1,AD=![]() ,∠BAC的平分线交BC于点D,M是AD上的动点,连接BM、MN,则BM+MN的最小值是( )
,∠BAC的平分线交BC于点D,M是AD上的动点,连接BM、MN,则BM+MN的最小值是( )
A. ![]() B. 2C. 1D. 3
B. 2C. 1D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,对于点P(a,b),若点P′的坐标为(a ![]() ,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k关联点”.
,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k关联点”.
(1)求点P(﹣2,3)的“2关联点”P′的坐标;
(2)若a、b为正整数,点P的“k关联点”P′的坐标为(3,6),求出k及点P的坐标;
(3)如图,点Q的坐标为(0,4 ![]() ),点A在函数y=﹣
),点A在函数y=﹣ ![]() (x<0)的图象上运动,且点A是点B的“﹣
(x<0)的图象上运动,且点A是点B的“﹣ ![]() 关联点”,当线段BQ最短时,求B点坐标.
关联点”,当线段BQ最短时,求B点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雾霾天气严重影响市民的生活质量.在去年寒假期间,某校八年级一班的综合实践小组同学对“雾霾天气的主要成因”随机调查了所在城市部分市民.并对调查结果进行了整理.绘制了如图不完整的统计图表.观察分析并回答下列问题.
组别 | 雾霾天气的主要成因 | 百分比 |
A | 工业污染 | 45% |
B | 汽车尾气排放 | m |
C | 炉烟气排放 | 15% |
D | 其他(滥砍滥伐等) | n |
(1)本次被调查的市民共有多少人?
(2)求m、n的值,并计算图2中区域B所对应的扇形圆心角的度数;
(3)若该市有100万人口,请估计持有A、B两组主要成因的市民有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),C(﹣1,2),且![]() .
.
(1)求a,b的值;
(2)y轴上是否存在一点M,使△COM的面积是△ABC的面积的一半,求点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com