
����Ŀ����2016����˫ʮһ���ڼ䣬ij��ݹ�˾�ƻ����üס������ֳ�����ݻ���ӻ����������㣺���������ֳ������ˣ�10�������������������������ֳ������������������ǵ������ü��ֳ����������������2����
(1)��ס������ֳ��������������ֱ���Ҫ�����죿
(2)��֪���üס������ֳ������������65000Ԫ�����ֳ���ÿ����������ֳ���ÿ�������1500Ԫ�����ʣ���������ֳ�������������ֳ��������������ֳ���������������У���һ��������٣���˵�����ɣ�
���𰸡�(1)�ס������������������ֱ���Ҫ15�죬30�죻(2)������.
��������
��1������������Եõ���Ӧ�ķ�ʽ���̣��Ӷ����Խ���⣻��2����������͵ڣ�1�����еĽ�����Էֱ�������ַ�ʽ�ķ��ã��Ӷ����Խ���⣮
��1����׳��������������Ҫx�죬���ҳ��������������Ҫ2x�죬
��![]() ����10=1
����10=1
��ã�x=15
��2x=30
���ס������������������ֱ���Ҫ15�죬30�죻
��2����׳������ÿ��aԪ�����ҳ������ÿ�죨a-1500��Ԫ��
[a+��a-1500��]��10=65000
��ã�a=4000
��a-1500=2500
��������׳�ʱ�����Ϊ��15��4000=60000��
���������ҳ�ʱ�����Ϊ��30��2500=75000��
��60000��65000��75000��
��������׳�������٣�


 ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�
ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
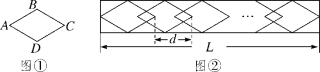
����Ŀ��ij������·���������β����������ɸ�������ABCD(��ͼ��)ȫ�ȵ�ͼ����ɵģ�ÿ����һ�����Σ����γ��Ⱦ�����dcm(��ͼ��)����֪����ABCD�ı߳�Ϊ6![]() cm����BAD��60��.
cm����BAD��60��.
(1)��AC�ij���
(2)��d��15cm�������ܳ���LΪ3918cm������Ҫ���ٸ�����������ͼ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=x2+bx+c��x�ύ��A��B���㣬B������Ϊ��3��0������y�ύ�ڵ�C��0����3��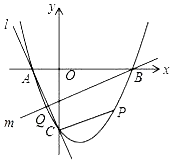
��1���������ߵĽ���ʽ��
��2����P��������λ�ڵ������IJ������˶������ı���ABPC��������ʱ�����P������
��3��ֱ��l����A��C���㣬��Q��������λ��y�����IJ������˶���ֱ��m������B�͵�Q���Ƿ����ֱ��m��ʹ��ֱ��l��m��x��Χ�ɵ������κ�ֱ��l��m��y��Χ�ɵ����������ƣ������ڣ����ֱ��m�Ľ���ʽ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
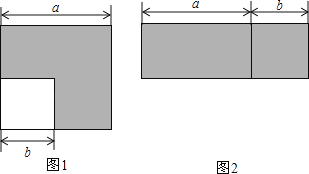
����Ŀ����ͼ1��ʾ���߳�Ϊa������������һ���߳�Ϊb��С�����Σ���ͼ2��ʾ����ͼ1����Ӱ����ƴ�ɵ�һ�������Σ�
��1����ͼ1����Ӱ�������ΪS1��ͼ2����Ӱ�������ΪS2����ֱ���ú�a��b�Ĵ���ʽ��ʾS1��S2��
��2����д��������������ʾ�ij˷���ʽ��
��3�������������ʽ���㣺��2+1����22+1����24+1����28+1��+1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ϵ�A��C��Ӧ�����ֱ�Ϊa��c����a��c������|a+4|+��c��1��2018=0����O��Ӧ����Ϊ0����B��Ӧ����Ϊ��3��
��1������a��c��ֵ��
��2����A��B������ͬʱ�������������˶�����A�ٶ�Ϊ2����λ����/�룬��B�ٶ�Ϊ1����λ����/�룬�����A�ϵ�B��
��3���ڣ�2���������£����˶�ʱ��Ϊt�룬�˶������У���A��B���㵽ԭ��O�ľ������ʱ����t��ֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
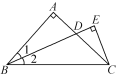
����Ŀ����ͼ������ABC����AB��AC����BAC��90�㣬��1����2��CE��BD��BD���ӳ����ڵ�E.��֤��BD��2CE.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ȫ�ȵġ�ABC�͡�DEF�ص���һ�𣬹̶���ABC������DEF�������±任��
��1����ͼ1����DEF��ֱ��CB����ƽ�ƣ�����F���߶�CB���ƶ���������AF��AD��BD����ֱ��д��S��ABC��S�ı���AFBD�Ĺ�ϵ��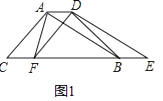
��2����ͼ2������Fƽ�Ƶ��߶�BC���е�ʱ���ı���AFBD��ʲô�����ı��Σ������֤����
��3������Fƽ�Ƶ��߶�BC���е�ʱ�����ı���AFBDΪ�����Σ������ABCӦ����ʲô��������ֱ��д�����ۣ��ڴ������£�����DEF��DF�۵�����E����FA���ӳ����ϵĵ�G��������CG������ͼ3λ�û���ͼ�Σ������sin��CGF��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
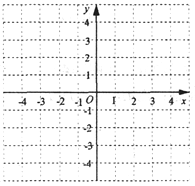
����Ŀ����������y=2x+4��ͼ�����ͼ�����������⣺
(1)д������2x+4=0�Ľ⣻
(2)����4��yʱ������Ӧx��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com