
【题目】如图,数轴上点A、C对应的数分别为a、c,且a、c,满足|a+4|+(c﹣1)2018=0,点O对应的数为0,点B对应的数为﹣3.
(1)求数a、c的值;
(2)点A,B沿数轴同时出发向右匀速运动,点A速度为2个单位长度/秒,点B速度为1个单位长度/秒,几秒后,点A追上点B;
(3)在(2)的条件下,若运动时间为t秒,运动过程中,当A,B两点到原点O的距离相等时,求t的值.
![]()
【答案】(1)a的值是﹣4,c的值是1,(2)1秒后,点A追上点B,(3)A,B两点到原点O的距离相等时,t的值为1或![]() .
.
【解析】
(1)根据绝对值与偶次方的非负性即可求出a,c的值;
(2)根据AB=1,AO=4,BO=3,设x秒后,点A追上点B,则2x﹣x=1,解得x=1;
(3)根据AB=1,AO=4,BO=3,分当A、B在原点的左侧相遇与在异侧到原点O的距离相等两种情况进行求解即可.
解:(1)由题意,得 a+4=0,c﹣1=0,
解得:a=﹣4,c=1.
答:a的值是﹣4,c的值是1
(2)∵点B对应的数为﹣3,A对应的数是﹣4,
∴AB=1,AO=4,BO=3.
设x秒后,点A追上点B,依题意有
2x﹣x=1 解得x=1;
∴1秒后,点A追上点B
(3)∵点B对应的数为﹣3,A对应的数是﹣4,
∴AB=1,AO=4,BO=3.
当A、B在原点的左侧A、B相遇时,
2t﹣t=1, 解得: t=1,
当A、B在原点的异侧时,
2t﹣4=3﹣t, 解得:t=![]() .
.
∴A,B两点到原点O的距离相等时,t的值为1或![]() .
.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】在实数范围内定义一种运算“*”,其运算法则为a*b=a2﹣ab.根据这个法则,下列结论中正确的是_______.(把所有正确结论的序号都填在横线上)
①![]() *
*![]() =2﹣
=2﹣![]() ;②若a+b=0,则a*b=b*a;③(x+2)*(x+1)=0是一元二次方程;④方程(x+3)*1=1的根是x1=
;②若a+b=0,则a*b=b*a;③(x+2)*(x+1)=0是一元二次方程;④方程(x+3)*1=1的根是x1=![]() ,x2=
,x2=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在平面直角坐标系中,![]() OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+b将
OABC的边OC落在x轴的正半轴上,且点C(4,0),B(6,2),直线y=2x+b将![]() OABC的面积平分,则b=_______.
OABC的面积平分,则b=_______.
(2)在平面直角坐标系中,直线y=2x+3关于原点对称的直线的表达式为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年“双十一”期间,某快递公司计划租用甲、乙两种车辆快递货物,从货物量来计算:若租用两种车辆合运,10天可以完成任务;若单独租用乙种车辆,完成任务的天数是单独租用甲种车辆完成任务天数的2倍.
(1)求甲、乙两种车辆单独完成任务分别需要多少天?
(2)已知租用甲、乙两种车辆合运需租金65000元,甲种车辆每天的租金比乙种车辆每天的租金多1500元,试问:租甲和乙两种车辆、单独租甲种车辆、单独租乙种车辆这三种租车方案中,哪一种租金最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】金湖中学社团活动开展地丰富多彩.七年级数学社团课上同学们在探究一数值转换器,原理如图所示.开始输入x值为5,可发现第一次输出的结果是8,第2次输出结果是4,依次下去…,第2018次输出的结果是__.
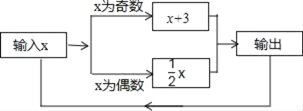
查看答案和解析>>
科目:初中数学 来源: 题型:
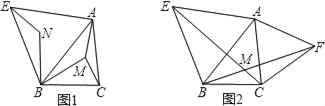
【题目】如图①,点M为锐角三角形ABC内任意一点,连接AM、BM、CM.以AB为一边向外作等边三角形△ABE,将BM绕点B逆时针旋转60°得到BN,连接EN.
(1)求证:△AMB≌△ENB;
(2)若AM+BM+CM的值最小,则称点M为△ABC的费马点.若点M为△ABC的费马点,试求此时∠AMB、∠BMC、∠CMA的度数;
(3)小翔受以上启发,得到一个作锐角三角形费马点的简便方法:如图②,分别以△ABC的AB、AC为一边向外作等边△ABE和等边△ACF,连接CE、BF,设交点为M,则点M即为△ABC的费马点.试说明这种作法的依据.
查看答案和解析>>
科目:初中数学 来源: 题型:
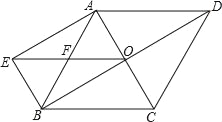
【题目】如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)求证:EO=DC;
(2)若菱形ABCD的边长为10,∠EBA=60°,求:菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
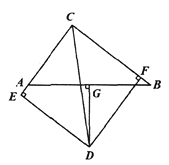
【题目】如图,△ABC中,AC=6,BC=8,AB=10,∠BCA的平分线与AB的垂直平分线DG交于点D,DE⊥CA的延长线于点E,DF⊥CB于点F.
(1)判断△ABC的形状,并说明理由;
(2)求证:AE=BF;
(3)求DG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com