
����Ŀ����ͼ������MΪ���������ABC������һ�㣬����AM��BM��CM����ABΪһ���������ȱ���������ABE����BM�Ƶ�B��ʱ����ת60���õ�BN������EN��
��1����֤����AMB�ա�ENB��
��2����AM+BM+CM��ֵ��С����Ƶ�MΪ��ABC�ķ����㣮����MΪ��ABC�ķ����㣬�����ʱ��AMB����BMC����CMA�Ķ�����
��3��С���������������õ�һ������������η�����ļ�㷽������ͼ�����ֱ�����ABC��AB��ACΪһ���������ȱ���ABE�͵ȱ���ACF������CE��BF���轻��ΪM�����M��Ϊ��ABC�ķ����㣮��˵���������������ݣ�
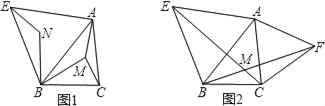
���𰸡���1������������2����BMC =120�㣻��AMB =120�㣻��AMC=120�㣻��3���߶�EC��BF�Ľ��㼴Ϊ��ABC�ķ����㣮
��������
(1)��ϵȱ������ε����ʣ�����SAS��֤��AMB�ա�ENB��
(2)����MN����(1)�Ľ���֤����BMNΪ�ȱ������Σ�����BM=MN����AM+BM+CM=EN+MN+CM�����Ե�E��N��M��C�ĵ㹲��ʱ��AM+BM+CM��ֵ��С���Ӷ������ʱ��AMB����BMC����CMA�Ķ�����
(3)����(2)�з�����Ķ��壬����ABC�ķ��������߶�EC�ϣ�ͬ��Ҳ���߶�BF�ϣ�����߶�EC��BF�Ľ��㼴Ϊ��ABC�ķ�����.
��1��֤�����ߡ�ABEΪ�ȱ������Σ�
��AB=BE����ABE=60�㣮
����MBN=60�㣬
���ABM=��EBN��
����AMB����ENB��
��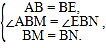
���AMB�ա�ENB��SAS����
��2������MN��
�ɣ�1��֪��AM=EN��
�ߡ�MBN=60�㣬BM=BN��
���BMNΪ�ȱ������Σ�
��BM=MN��
��AM+BM+CM=EN+MN+CM��
����E��N��M��C�ĵ㹲��ʱ��AM+BM+CM��ֵ��С��
��ʱ����BMC=180�㩁��NMB=120�㣻
��AMB=��ENB=180�㩁��BNM=120�㣻
��AMC=360�㩁��BMC����AMB=120�㣮
��3���ɣ�2��֪����ABC�ķ��������߶�EC�ϣ�ͬ��Ҳ���߶�BF�ϣ�
����߶�EC��BF�Ľ��㼴Ϊ��ABC�ķ����㣮
�ʴ�Ϊ����1������������2����BMC =120������AMB =120������AMC=120������3���߶�EC��BF�Ľ��㼴Ϊ��ABC�ķ����㣮


 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABOC�Ķ���O������ԭ�㣬��BO��x��ĸ������ϣ���BOC=60�㣬����C������Ϊ��m��3 ![]() ��������������y=
��������������y= ![]() ��ͼ�������ζԽ���AO��D�㣬����BD����DB��x��ʱ��k��ֵ�ǣ� ��
��ͼ�������ζԽ���AO��D�㣬����BD����DB��x��ʱ��k��ֵ�ǣ� ��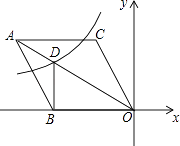
A.6 ![]()
B.��6 ![]()
C.12 ![]()
D.��12 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=x2+bx+c��x�ύ��A��B���㣬B������Ϊ��3��0������y�ύ�ڵ�C��0����3��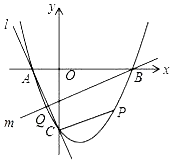
��1���������ߵĽ���ʽ��
��2����P��������λ�ڵ������IJ������˶������ı���ABPC��������ʱ�����P������
��3��ֱ��l����A��C���㣬��Q��������λ��y�����IJ������˶���ֱ��m������B�͵�Q���Ƿ����ֱ��m��ʹ��ֱ��l��m��x��Χ�ɵ������κ�ֱ��l��m��y��Χ�ɵ����������ƣ������ڣ����ֱ��m�Ľ���ʽ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ϵ�A��C��Ӧ�����ֱ�Ϊa��c����a��c������|a+4|+��c��1��2018=0����O��Ӧ����Ϊ0����B��Ӧ����Ϊ��3��
��1������a��c��ֵ��
��2����A��B������ͬʱ�������������˶�����A�ٶ�Ϊ2����λ����/�룬��B�ٶ�Ϊ1����λ����/�룬�����A�ϵ�B��
��3���ڣ�2���������£����˶�ʱ��Ϊt�룬�˶������У���A��B���㵽ԭ��O�ľ������ʱ����t��ֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
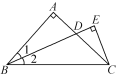
����Ŀ����ͼ������ABC����AB��AC����BAC��90�㣬��1����2��CE��BD��BD���ӳ����ڵ�E.��֤��BD��2CE.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ı���ABCD�У�AC��BD��AB��AD��Ҫʹ�ı���ABCD�����Σ�ֻ������һ���������������������_____��ֻҪ��дһ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ȫ�ȵġ�ABC�͡�DEF�ص���һ�𣬹̶���ABC������DEF�������±任��
��1����ͼ1����DEF��ֱ��CB����ƽ�ƣ�����F���߶�CB���ƶ���������AF��AD��BD����ֱ��д��S��ABC��S�ı���AFBD�Ĺ�ϵ��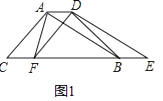
��2����ͼ2������Fƽ�Ƶ��߶�BC���е�ʱ���ı���AFBD��ʲô�����ı��Σ������֤����
��3������Fƽ�Ƶ��߶�BC���е�ʱ�����ı���AFBDΪ�����Σ������ABCӦ����ʲô��������ֱ��д�����ۣ��ڴ������£�����DEF��DF�۵�����E����FA���ӳ����ϵĵ�G��������CG������ͼ3λ�û���ͼ�Σ������sin��CGF��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijʳƷ���������Ĵ�װʳƷ�г����Ʒ20�������ÿ���������Ƿ���ϱ�����������IJ��ֱַ���������������ʾ����¼���±���
��������IJ�ֵ |
|
| 0 | 1 | 3 | 6 |
�� �� | 1 | 4 | 3 | 4 | 5 | 3 |
��1��������Ʒ��ƽ�������ȱ���������٣�����ټ��ˣ�
��2����ÿ��������Ϊ450�ˣ�����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��CD��CE��AB�ڵ�F������E=20������C=45�������A�Ķ���Ϊ��������

A. 5�� B. 15�� C. 25�� D. 35��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com