
【题目】两个全等的△ABC和△DEF重叠在一起,固定△ABC,将△DEF进行如下变换:
(1)如图1,△DEF沿直线CB向右平移(即点F在线段CB上移动),连接AF、AD、BD,请直接写出S△ABC与S四边形AFBD的关系;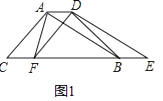
(2)如图2,当点F平移到线段BC的中点时,四边形AFBD是什么特殊四边形?请给出证明;
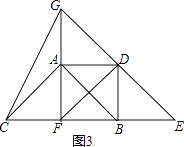
(3)当点F平移到线段BC的中点时,若四边形AFBD为正方形,猜想△ABC应满足什么条件?请直接写出结论:在此条件下,将△DEF沿DF折叠,点E落在FA的延长线上的点G处,连接CG,请在图3位置画出图形,并求出sin∠CGF的值.
【答案】
(1)解:S△ABC=S四边形AFBD,理由如下:
由题意可得:AD∥EC,
则S△ADF=S△ABD,
故S△ACF=S△ADF=S△ABD,
则S△ABC=S四边形AFBD;
(2)解:当点F平移到线段BC的中点时,四边形AFBD是平行四边形,理由如下:
∵F为BC的中点,
∴CF=BF,
∵CF=AD,
∴AD=BF,由平移可知AD∥BF,
∴四边形AFBD为平行四边形;
(3)解:如图3所示:△ABC为等腰直角三角形,即AB=AC,∠BAC=90°;理由如下:
由(2)得:四边形AFBD是平行四边形,
∵AB=AC,F为BC的中点,
∴AF⊥BC,
∴平行四边形AFBD为矩形,
∵∠BAC=90°,F为BC的中点,
∴AF= ![]() BC=BF,
BC=BF,
∴四边形AFBD是正方形;
设CF=k,则GF=EF=CB=2k,
由勾股定理得:CG= ![]() =
= ![]() k,
k,
sin∠CGF= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)利用平行线的性质以及三角形面积关系得出答案;(2)证出AD=BF,由平移可知AD∥BF,利用平行四边形的判定得出四边形AFBD为平行四边形即可;(3)根据题意画出图形,由等腰三角形的性质得出AF⊥BC,证出平行四边形AFBD为矩形,由直角三角形斜边上的中线性质得出AF= ![]() BC=BF,得出四边形AFBD是正方形;设CF=k,则GF=EF=CB=2k,由勾股定理求出CG,利用sin∠CGF=
BC=BF,得出四边形AFBD是正方形;设CF=k,则GF=EF=CB=2k,由勾股定理求出CG,利用sin∠CGF= ![]() 求出即可.
求出即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为30米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米. 
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年“双十一”期间,某快递公司计划租用甲、乙两种车辆快递货物,从货物量来计算:若租用两种车辆合运,10天可以完成任务;若单独租用乙种车辆,完成任务的天数是单独租用甲种车辆完成任务天数的2倍.
(1)求甲、乙两种车辆单独完成任务分别需要多少天?
(2)已知租用甲、乙两种车辆合运需租金65000元,甲种车辆每天的租金比乙种车辆每天的租金多1500元,试问:租甲和乙两种车辆、单独租甲种车辆、单独租乙种车辆这三种租车方案中,哪一种租金最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
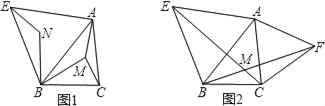
【题目】如图①,点M为锐角三角形ABC内任意一点,连接AM、BM、CM.以AB为一边向外作等边三角形△ABE,将BM绕点B逆时针旋转60°得到BN,连接EN.
(1)求证:△AMB≌△ENB;
(2)若AM+BM+CM的值最小,则称点M为△ABC的费马点.若点M为△ABC的费马点,试求此时∠AMB、∠BMC、∠CMA的度数;
(3)小翔受以上启发,得到一个作锐角三角形费马点的简便方法:如图②,分别以△ABC的AB、AC为一边向外作等边△ABE和等边△ACF,连接CE、BF,设交点为M,则点M即为△ABC的费马点.试说明这种作法的依据.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:等腰三角形OAB在直角坐标系中的位置如下图,点A的坐标为( ![]() ,3),点B的坐标为(﹣6,0).
,3),点B的坐标为(﹣6,0). 
(1)若△OAB关于y轴的轴对称图形是△OA'B',请直接写出A、B的对称点A'、B'的坐标;
(2)若将△OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数 ![]() 的图象上,求a的值;
的图象上,求a的值;
(3)若△OAB绕点O按逆时针方向旋转30°,此时点B恰好落在反比例函数 ![]() 的图象上,求k的值.
的图象上,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
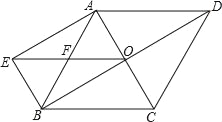
【题目】如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)求证:EO=DC;
(2)若菱形ABCD的边长为10,∠EBA=60°,求:菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数y= ![]() (k1>0,x>0)、函数y=
(k1>0,x>0)、函数y= ![]() (k2<0,x<0)的图象分别经过OABC的顶点A、C,点B在y轴正半轴上,AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为( )
(k2<0,x<0)的图象分别经过OABC的顶点A、C,点B在y轴正半轴上,AD⊥x轴于点D,CE⊥x轴于点E,若|k1|:|k2|=9:4,则AD:CE的值为( )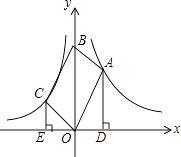
A.4:9
B.2:3
C.3:2
D.9:4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请完成下面的解答过程.
如图,∠1=∠B,∠C=110°,求∠3的度数.
解:∵∠1=∠B,
∴AD∥ .( )
∴∠C+ =180°.(两直线平行,同旁内角互补)
∵∠C=110°,
∴∠2= °.
∴∠3= =70°.( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,AB边上的高CD=4,点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动,当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).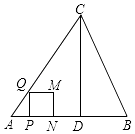
(1)直接写出tanB的值为 .
(2)求点M落在边BC上时t的值.
(3)当正方形PQMN与△ABC重叠部分为四边形时,求S与t之间的函数关系式.
(4)边BC将正方形PQMN的面积分为1:3两部分时,直接写出t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com