
����Ŀ����ͼ���ڡ�ABC�У�AB=AC=5��AB���ϵĸ�CD=4����P�ӵ�A��������AB��ÿ��3����λ���ȵ��ٶ����յ�B�˶�������P�����A��B�غ�ʱ������P��PQ��AB������AC���BC�ڵ�Q����PQΪ�����Ҳ���������PQMN����������PQMN���ABC�ص�����ͼ�ε����ΪS��ƽ����λ������P�˶���ʱ��Ϊt���룩��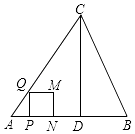
��1��ֱ��д��tanB��ֵΪ ��
��2�����M���ڱ�BC��ʱt��ֵ��
��3����������PQMN���ABC�ص�����Ϊ�ı���ʱ����S��t֮��ĺ�����ϵʽ��
��4����BC��������PQMN�������Ϊ1��3������ʱ��ֱ��д��t��ֵ��
���𰸡�
��1��2
��2���⣺����M����BC����ʱ����ͼ1��
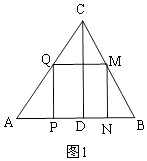
������ã�AP=3t��
tan��CAB= ![]() ��
��
��PQ=PN=MN=4t��BN=2t��
��3t+4t+2t=5��
t= ![]()
��3���⣺�����������
�ٵ�0��t�� ![]() ʱ����ͼ1��������PQMN���ABC�ص�������������PQMN��
ʱ����ͼ1��������PQMN���ABC�ص�������������PQMN��
��S=PQ2=��4t��2=16t2��
�ڵ�N��B�غ�ʱ����ͼ2��
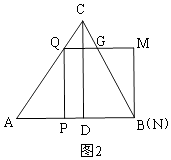
AP=3t��PQ=PB=4t��
��3t+4t=5��
t= ![]() ��
��
�� ![]() ��t��
��t�� ![]() ʱ����ͼ3��������PQMN���ABC�ص������������EQPNF��
ʱ����ͼ3��������PQMN���ABC�ص������������EQPNF��
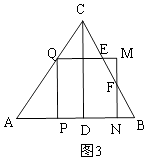
�۵� ![]() ��t��1ʱ����ͼ4��������PQMN���ABC�ص�����������EQPB��
��t��1ʱ����ͼ4��������PQMN���ABC�ص�����������EQPB��

��AP=3t��PN=4t��
��BN=7t��5��PB=4t����7t��5��=��3t+5��
��Rt��APQ��AQ=5t��
��QC=5��5t��
��AC=AB��
���ACB=��ABC��
��QE��AB��
���QEC=��ABC��
���QEC=��ACB��
��QE=QC=5��5t��
��S=S����QPBE= ![]() ��QE+PB����PQ��
��QE+PB����PQ��
= ![]() ��5��5t+5��3t����4t=��16t2+20t��
��5��5t+5��3t����4t=��16t2+20t��
����������S��t֮��ĺ�����ϵʽΪ��
S= 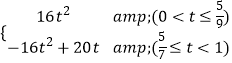
��4���⣺��ͼ2����t= ![]() ʱ��CQ=QG=5��5t=
ʱ��CQ=QG=5��5t= ![]() ��
��
��GM=4t�� ![]() =
= ![]() ��
��
��QG=GM��
��S��QGB=S��GMB��
��S����GQPB��S��GMB=3��1��
��P��D�غ�ʱ��t=1����ͼ5��
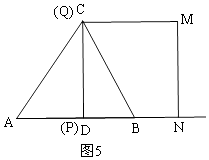
��S��CDB��S�ı���CBNM= ![]() ��2��4����42��
��2��4����42�� ![]() ��2��4����
��2��4����
=1��3��
����������t= ![]() s��1sʱ����BC��������PQMN�������Ϊ1��3������
s��1sʱ����BC��������PQMN�������Ϊ1��3������
���������⣺��1����CD��AB��
���ADC=��ADB=90�㣬
����Rt��ACD��AD= ![]() =3��
=3��
��BD=AB��AD=5��3=2��
����Rt��BCD��tan��B= ![]() =
= ![]() =2��
=2��
���Դ���2��
�����㾫����ͨ��������ù��ɶ����ĸ���������ε����ʣ�����ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2���������ĸ��Ƕ���ֱ�ǣ������߶���ȣ������ε������Խ�����ȣ����һ��ഹֱƽ�֣�ÿ���Խ���ƽ��һ��Խǣ������ε�һ���Խ��߰������ηֳ�����ȫ�ȵĵ���ֱ�������Σ������εĶԽ�����ߵļн���45o�������ε������Խ��߰���������ηֳ��ĸ�ȫ�ȵĵ���ֱ�������μ����Խ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ȫ�ȵġ�ABC�͡�DEF�ص���һ�𣬹̶���ABC������DEF�������±任��
��1����ͼ1����DEF��ֱ��CB����ƽ�ƣ�����F���߶�CB���ƶ���������AF��AD��BD����ֱ��д��S��ABC��S�ı���AFBD�Ĺ�ϵ��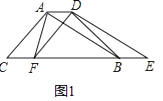
��2����ͼ2������Fƽ�Ƶ��߶�BC���е�ʱ���ı���AFBD��ʲô�����ı��Σ������֤����
��3������Fƽ�Ƶ��߶�BC���е�ʱ�����ı���AFBDΪ�����Σ������ABCӦ����ʲô��������ֱ��д�����ۣ��ڴ������£�����DEF��DF�۵�����E����FA���ӳ����ϵĵ�G��������CG������ͼ3λ�û���ͼ�Σ������sin��CGF��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y=2x+4��ͼ�����ͼ�����������⣺
(1)д������2x+4=0�Ľ⣻
(2)����4��yʱ������Ӧx��ȡֵ��Χ��
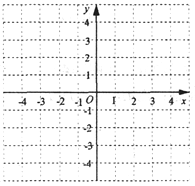
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��CD��CE��AB�ڵ�F������E=20������C=45�������A�Ķ���Ϊ��������

A. 5�� B. 15�� C. 25�� D. 35��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�����OABC�У�OΪƽ��ֱ������ϵ��ԭ�㣬��A����C�ֱ���x�ᣬy���ϣ���B����Ϊ��4��6������P�ӵ�O��������ÿ��2����λ���ȵ��ٶ���O��C��B�����˶�������Bֹͣ�����P�˶���ʱ��Ϊt���룩��
��1����A����������������
��2����t=1��ʱ����P����������������
��3������P��OC���˶�����ֱ��д����P�����꣨�ú���t��ʽ�ӱ�ʾ����
��4�����ƶ������У�����P��y��ľ���Ϊ1����λ����ʱ����t��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�AB=AC����BAC=100�㣬��D��BC���ϣ���ABD����AFD����ֱ��AD�Գƣ���FAC��ƽ���߽�BC�ڵ�G������FG��
��1������DFG�Ķ�����
��2������BAD=�ȣ�
������Ϊ��ֵʱ����DFGΪ���������Σ�
����DFG�п�����ֱ�������������У��������Ӧ�Ħ�ֵ����û�У���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ٰ���ӭʡ����ѧ���黭չ������Ҫ�ڳ�����չ���л���![]() ����״����С��ȫһ����С������(����Ӱ����)���ǰڷ�չ����Ʒ��
����״����С��ȫһ����С������(����Ӱ����)���ǰڷ�չ����Ʒ��
��1����ͼ1�������εij��Ϳ��քeΪ![]() ��
��![]() �ף���С�����εij��Ϳ���
�ף���С�����εij��Ϳ���

��2����ͼ2�������εij��Ϳ��ֱ�Ϊ![]() ��
��![]() �����һ��С��������һ�������ܳ��ı�ֵ��
�����һ��С��������һ�������ܳ��ı�ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC����A=120![]() ��BC=6cm��AB�Ĵ�ֱƽ���߽�BC�ڵ�M����AB�ڵ�E��AC�Ĵ�ֱƽ���߽�BC�ڵ�N����AC�ڵ�F����MN�ij�Ϊ�� ��
��BC=6cm��AB�Ĵ�ֱƽ���߽�BC�ڵ�M����AB�ڵ�E��AC�Ĵ�ֱƽ���߽�BC�ڵ�N����AC�ڵ�F����MN�ij�Ϊ�� ��

A. 1.5cm B. 2cm C. 2.5cm D. 3cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABD�͡�BDC��ƽ���߽��ڵ�E��BE��CD�ڵ�F����1+��2=90����
��1����˵����AB��CD��
��2����̽����2���3��������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com