
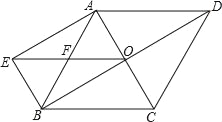
【题目】如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)求证:EO=DC;
(2)若菱形ABCD的边长为10,∠EBA=60°,求:菱形ABCD的面积.
【答案】(1)见解析;(2)50![]()
【解析】
(1)首先证明四边形AEBO是平行四边形,再证明是矩形可得EO=AB,又因为AB=CD,所以EO=DC,问题得证;(2)根据菱形ABCD的面积=△ABD的面积+△BCD的面积=2×△ABD的面积计算即可.
(1)证明:∵BE∥AC,AE∥BD
∴四边形AEBO是平行四边形
又∵菱形ABCD对角线交于点O
∴AC⊥BD
即∠AOB=90°
∴四边形AEBO是矩形
∴EO=AB
∵四边形ABCD是菱形
∴AB=DC
∴EO=DC.
(2)解:由(1)知四边形AEBO是矩形
∴∠EBO=90°
∵∠EBA=60°
∴∠ABO=30°
在Rt△ABO中,AB=10,∠ABO=30°
∴AO=5,BO=5![]()
∴BD=10![]()
∴菱形ABCD的面积=△ABD的面积+△BCD的面积
=2×△ABD的面积
=2×![]() ×10
×10![]() ×5
×5
=50![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点D是 ![]() 上一点,且∠BDE=∠CBE,BD与AE交于点F.
上一点,且∠BDE=∠CBE,BD与AE交于点F. 
(1)求证:BC是⊙O的切线;
(2)若BD平分∠ABE,求证:DE2=DFDB;
(3)在(2)的条件下,延长ED,BA交于点P,若PA=AO,DE=2,求PD的长和⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上点A、C对应的数分别为a、c,且a、c,满足|a+4|+(c﹣1)2018=0,点O对应的数为0,点B对应的数为﹣3.
(1)求数a、c的值;
(2)点A,B沿数轴同时出发向右匀速运动,点A速度为2个单位长度/秒,点B速度为1个单位长度/秒,几秒后,点A追上点B;
(3)在(2)的条件下,若运动时间为t秒,运动过程中,当A,B两点到原点O的距离相等时,求t的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个全等的△ABC和△DEF重叠在一起,固定△ABC,将△DEF进行如下变换:
(1)如图1,△DEF沿直线CB向右平移(即点F在线段CB上移动),连接AF、AD、BD,请直接写出S△ABC与S四边形AFBD的关系;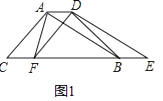
(2)如图2,当点F平移到线段BC的中点时,四边形AFBD是什么特殊四边形?请给出证明;
(3)当点F平移到线段BC的中点时,若四边形AFBD为正方形,猜想△ABC应满足什么条件?请直接写出结论:在此条件下,将△DEF沿DF折叠,点E落在FA的延长线上的点G处,连接CG,请在图3位置画出图形,并求出sin∠CGF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于BC的一半长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连结CD,若AC=5,AB=11,则△ACD的周长为( )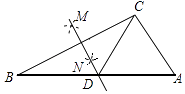
A.11
B.16
C.21
D.27
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值 |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x﹣4与x轴、y轴分别交于M、N两点,以坐标原点O为圆心的⊙O半径为2,将⊙O沿x轴向右平移,当⊙O恰好与直线MN相切时,平移的最小距离为 . 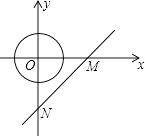
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,△ABD和△AFD关于直线AD对称,∠FAC的平分线交BC于点G,连接FG.
(1)求∠DFG的度数;
(2)设∠BAD=θ,
①当θ为何值时,△DFG为等腰三角形;
②△DFG有可能是直角三角形吗?若有,请求出相应的θ值;若没有,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com