
【题目】如图,点A,B是数轴上的两个点,点A表示的数为﹣2,点B在点A右侧,距离A点12个单位长度,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.

(1)填空:①数轴上点B表示的数为 ;
②数轴上点P表示的数为 (用含t的代数式表示).
(2)设AP和PB的中点分别为点M,N,在点P的运动过程中,线段M N的长度是否发生变化?若变化,请说明理由;若不变,求出线段M N的长.
【答案】(1)①数轴上点B表示的数为10;②数轴上点P表示的数为 (2t﹣2);(2)线段MN的长度不发生变化,值为6.
【解析】
(1)①利用两点之间的距离计算方法求得点B所表示的数即可;
②利用左减右加的规律求得点P的所表示的数即可;
(2)分类讨论:①当点P在点A、B两点之间运动时,②当点P运动到点B的右侧时,③点P运动到点B时,利用中点的定义和线段的和差易求出MN.
解:(1)①∵10-(-2)=12,
∴数轴上点B表示的数为10;
②数轴上点P表示的数为(2t﹣2);
(2)线段MN的长度不发生变化.
①如图,当点P在点A、B之间运动时,
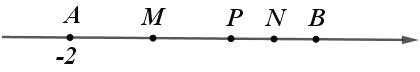
MN = MP + NP =![]() AP + PB =
AP + PB =![]() AB =
AB =![]() ×12 = 6;
×12 = 6;
②当点P运动到点B的右侧时,
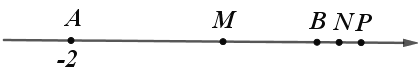
MN = MP﹣PB = ![]() AP﹣
AP﹣![]() BP =
BP = ![]() (AP﹣PB)
(AP﹣PB)
= ![]() AB =
AB = ![]() ×12 = 6;
×12 = 6;
③当点P运动到点B时,MN = MB = ![]() AB =
AB = ![]() ×12 = 6;
×12 = 6;
综上所述,线段MN的长度不发生变化,值为6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
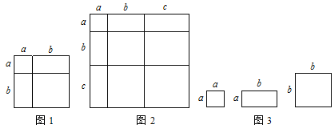
【题目】(知识生成)我们知道,用两种不同的方法计算同一个几何图形的面积,可以得到一些代数恒等式.
例如:如图可以得到(a+b)2=a2+2ab+b2,基于此,请解答下列问题:
⑴ 根据如图,写出一个代数恒等式:
![]() ;
;
⑵ 利用⑴中得到的结论,解决下面的问题:若a+b+c=12,![]() ,
,
则![]() ;
;
⑶ 小明同学用如图中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片拼出一个面积为(2a+b)(a+3b)的长方形,则x+y+z= ;
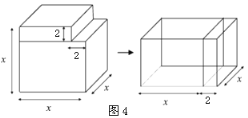
(知识迁移)⑷ 类似地,用两种不同的方法计算几何体的体积同样可以得到一些代数恒等式.如图表示的是一个边长为x的正方体挖去一个边长为2的小长方体后重新拼成一个新长方体.请你根据如图中两个图形的变化关系,写出一个代数恒等式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P点是灯塔所在位置,轮船A位于灯塔南偏东40°方向,轮船B位于灯塔北偏东30°方向,轮船C位于灯塔北偏西70°方向,航线PE(射线)平分∠BPC.
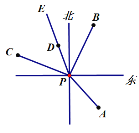
(1)求∠APE的度数;
(2)航线PE上的轮船D相对于灯塔P的方位是什么?
(以正北、正南方向为基准).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=kx+b(k≠0)与x轴、y轴分别交于A、B两点,与直线l2:y=3x交于点C,其中点C的坐标为(![]() ,c),点B的坐标为(0,3).
,c),点B的坐标为(0,3).
(1)求点C的坐标;
(2)求直线l1的表达式;
(3)在x轴上有一点D(3,0),求△BCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电力公司为鼓励市民节约用电,采取按月用电量分段收费办法.若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
(1) 分别写出当0≤x≤100和x>100时,y与x的函数关系式
(2) 利用函数关系式,说明电力公司采取的收费标准
(3) 若该用户某月用电62度,则应缴费多少元?若该用户某月缴费105元时,则该用户该月用了多少度电?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com