
【题目】如图,P点是灯塔所在位置,轮船A位于灯塔南偏东40°方向,轮船B位于灯塔北偏东30°方向,轮船C位于灯塔北偏西70°方向,航线PE(射线)平分∠BPC.
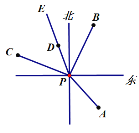
(1)求∠APE的度数;
(2)航线PE上的轮船D相对于灯塔P的方位是什么?
(以正北、正南方向为基准).
【答案】(1)160°;(2)轮船D在灯塔P北偏西20°的方位上
【解析】
(1)先求出∠BPC的度数,根据角平分线的定义,得∠BPE的度数,再求出∠APB的度数,进而即可求解;
(2)求出∠MPD的度数,进而即可求解.
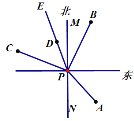
(1)∵∠NPA = 40°, ∠MPB = 30°,∠MPC = 70°,
∴∠BPC = ∠MPB + ∠MPC = 30°+70°= 100°,
∵PE平分∠BPC,
∴∠BPE =![]() ∠BPC =
∠BPC =![]() ×100°=50°,
×100°=50°,
∴∠APB =180°-∠NPA-∠MPB = 180°-40°-30°=110°,
∴∠APE = ∠BPE + ∠APB = 50°+ 110°= 160° ,
(2)∵∠MPD = ∠BPE -∠MPB = 50°-30°= 20°,
∴轮船D在灯塔P北偏西20°的方位上 .


科目:初中数学 来源: 题型:
【题目】已知:线段![]() 、
、![]() 、
、![]() ;
;
求作:△ABC,使![]() ,
, ![]() ,
, ![]() ;
;

【答案】答案见解析
【解析】试题分析:先画出与![]() 相等的角,再画出
相等的角,再画出![]() 的长,连接
的长,连接![]() ,则
,则![]() 即为所求三角形.
即为所求三角形.
试题解析:如图所示:①先画射线BC,
②以α的顶点为圆心,任意长为半径画弧,分别交α的两边交于为A′,C′;
③以相同长度为半径,B为圆心,画弧,交BC于点F,以F为圆心,C′A′为半径画弧,交于点E;
④在BF上取点C,使CB=a,以B为圆心,c为半径画圆交BE的延长线于点A,连接AC,
结论:△ABC即为所求三角形.

【题型】解答题
【结束】
15
【题目】已知:线段![]() ,
, ![]() ,求作:
,求作: ![]() ,使
,使![]() ,
, ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
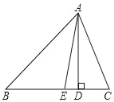
【题目】如图,在△ABC中,AD是BC边上的高,点E在BC上,AE是∠BAC的平分线,BE=AE,∠B=40°.
(1)求∠EAD的度数;
(2)求∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,AB=6,点C,D在⊙O上,且CD平分∠ACB,∠CAB=60°.
(1)求BC及阴影部分的面积;
(2)求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明是一个聪明而又富有想象力的孩子.学习了“有理数的乘方”后,他就琢磨着使用“乘方”这一数学知识脑洞大开地定义出“有理数的除方”概念.于是规定:若干个相同有理数(均不能为0)的除法运算叫做除方,如5÷5÷5,(﹣2)÷(﹣2)÷(﹣2)÷(﹣2)等,类比有理数的乘方.小明把5÷5÷5记作f(3,5),(﹣2)÷(﹣2)÷(﹣2)÷(﹣2)记作f(4,﹣2)
(1)直接写出计算结果,f(5,![]() )= ,f(6,3)= ;
)= ,f(6,3)= ;
(2)关于“有理数的除方”下列说法正确的是 (填序号)
①对于任何正整数n,都有f(n,﹣1)=1;
②f(6,3)=f(3,6);
③f(2,a)=1(a≠0);
④对于任何正整数n,都有f(2n,a)<0(a<0).
(3)小明深入思考后发现:“除方”运算能够转化成乘方运算,且结果可以写成幂的形式.请推导出“除方”的运算公式f(n,a)(n为正整数,a≠0,n≥2),要求写出推导过程将结果写成幂的形式(结果用含a,n的式子表示)
(4)请利用(3)问的推导公式计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B是数轴上的两个点,点A表示的数为﹣2,点B在点A右侧,距离A点12个单位长度,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.

(1)填空:①数轴上点B表示的数为 ;
②数轴上点P表示的数为 (用含t的代数式表示).
(2)设AP和PB的中点分别为点M,N,在点P的运动过程中,线段M N的长度是否发生变化?若变化,请说明理由;若不变,求出线段M N的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
(1)用含![]() 、
、![]() 的代数式表示地面总面积;
的代数式表示地面总面积;
(2)已知客厅面积比卫生间面积多21平方米,且地面总面积是卫生间面积的15倍.若铺1平方米地砖的平均费用为100元,那么铺地砖的总费用为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC
(2)若AB=4,AD=3 ![]() ,AE=3,求AF的长.
,AE=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年“双十一”期间,某快递公司计划租用甲、乙两种车辆快递货物,从货物量来计算:若租用两种车辆合运,10天可以完成任务;若单独租用乙种车辆,完成任务的天数是单独租用甲种车辆完成任务天数的2倍.
(1)求甲、乙两种车辆单独完成任务分别需要多少天?
(2)已知租用甲、乙两种车辆合运需租金65000元,甲种车辆每天的租金比乙种车辆每天的租金多1500元,试问:租甲和乙两种车辆、单独租甲种车辆、单独租乙种车辆这三种租车方案中,哪一种租金最少?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com