
����Ŀ��С����һ���������ָ����������ĺ��ӣ�ѧϰ�ˡ��������ij˷�����������ĥ��ʹ�á��˷�����һ��ѧ֪ʶ�Զ��ض�������������ij�����������ǹ涨�����ɸ���ͬ������(������Ϊ0)�ij������������������5��5��5��(��2)��(��2)��(��2)��(��2)�ȣ�����������ij˷���С����5��5��5����f(3��5)��(��2)��(��2)��(��2)��(��2)����f(4����2)
��1��ֱ��д����������f(5��![]() )=����������f(6��3)=����������
)=����������f(6��3)=����������
��2�����ڡ��������ij���������˵����ȷ������������(�����)
�������������n������f(n����1)=1��
��f(6��3)=f(3��6)��
��f(2��a)=1(a��0)��
�ܶ����κ�������n������f(2n��a)��0(a��0)��
��3��С������˼�����֣��������������ܹ�ת���ɳ˷����㣬�ҽ������д���ݵ���ʽ�����Ƶ����������������㹫ʽf(n��a)(nΪ��������a��0��n��2)��Ҫ��д���Ƶ����̽����д���ݵ���ʽ(����ú�a��n��ʽ�ӱ�ʾ)
��4�������ã�3���ʵ��Ƶ���ʽ���㣺![]() ��
��
���𰸡���1��8��![]() ����2���ۣ���3��f(n��a)
����2���ۣ���3��f(n��a)![]() (nΪ��������a��0��n��2)����4��
(n��������a��0��n��2)����4��![]() ��
��
��������
��1�����ݡ��������ij�����������㼴�ɣ�
��2�����ݡ��������ij�����������һ�жϼ��ɣ�
��3�����ݡ��������ij�����������㼴�ɣ�
��4�����ݣ�3���Ĺ�ʽ���㼴�ɣ�
�⣺��1��f(5��![]() )
)![]()
![]()
![]() 8��f(6��3)=3��3��3��3��3��3
8��f(6��3)=3��3��3��3��3��3![]() ��
��
�ʴ�Ϊ��8��![]() ��
��
��2���ٶ����κ�������n������f(n����1)=1��nΪ����ʱ��f(n����1)=��1���ٴ���
�ڡ�f(6��3)![]() ��f(3��6)
��f(3��6)![]()
��f(6��3)��f(3��6)���ڴ���
��f(2��a)=a��a=1(a��0)������ȷ��
�ܶ����κ�������n������f(2n��a)��0��������f(2n��a)��0(a��0)���ܴ���
�ʴ�Ϊ���ۣ�
��3����ʽf(n��a)=a��a��a��a�¡���a��a=1��(an��2)![]() (nΪ��������a��0��n��2)
(n��������a��0��n��2)
��4��![]()
=33��(![]() )2��23��(��4)3��(��2)4
)2��23��(��4)3��(��2)4
=27![]() (��64)��16
(��64)��16
![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С��С�ޣ�Сǿ������Ը��Ѫ�ߣ�����Ѫ��ΪO�ͣ�һ��Ѫ��ΪA�ͣ�����������������ѡһ����Ѫ�������Ժ��ִӴ�������������ѡһ����Ѫ��������������Ѫ��Ѫ�;�ΪO�͵ĸ��ʣ���Ҫ�����б�����״ͼ�ķ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ƽ���ڣ�ֱ��y=��x+5�� ![]() ���
��� ![]() ��ֱ���A��B���㣬���κ���y=
��ֱ���A��B���㣬���κ���y= ![]() +bx+c��ͼ����A��B���Ҷ���ΪC��
+bx+c��ͼ����A��B���Ҷ���ΪC��
��1����������κ����Ľ���ʽ��
��2����sin��OCA��ֵ��
��3����P��������κ���ͼ����λ��x���·���һ�㣬�� ![]() ABP�����Ϊ10�����P�����꣮
ABP�����Ϊ10�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����֧���̶Ӹ�10����Ա�����ߣ���λ��cm�����±���
�� | 179 | 177 | 178 | 177 | 178 | 178 | 179 | 179 | 177 | 178 |
�Ҷ� | 178 | 178 | 176 | 180 | 180 | 178 | 176 | 179 | 177 | 178 |
��1���Ӷ�Ա��ƽ������Ϊcm���ҶӶ�Ա��ƽ������Ϊcm��
��2��������ѧ����ͳ��֪ʶ�ж���֧���̶ӵ����߸�Ϊ�����أ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���֪��ABC�������������ֱ�ΪA����2��0����B����4��4����C��3����3����
��1��������ABC��
��2��������ABC����ƽ��3����λ���ȣ�������ƽ��4����λ���Ⱥ�õ�����A1B1C1��
��3�������A1B1C1�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��P���ǵ�������λ�ã��ִ�Aλ�ڵ�����ƫ��40�㷽���ִ�Bλ�ڵ�����ƫ��30�㷽���ִ�Cλ�ڵ�����ƫ��70�㷽����PE�����ߣ�ƽ�֡�BPC��
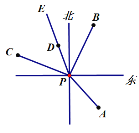
��1�����APE�Ķ�����
��2������PE�ϵ��ִ�D����ڵ���P�ķ�λ��ʲô��
�������������Ϸ���Ϊ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ ![]()
��1���������ߵĶԳ����� �� ����������
��2��ѡȡ�ʵ������������±�������ֱ������ϵ����㻭���������ߵ�ͼ��
x | �� | �� | |||||
y | �� | �� |

��3������������������A��x1 �� y1����B��x2 �� y2���ĺ���������x1��x2��1���ԱȽ�y1��y2�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��AB��CD��ֱ��EF�ֱ���AB��CD���ڵ�M��N����H��ֱ��CD�ϣ�HG��EF�ڵ�G������G��GP��AB�������н��ۣ��١�AMF����DNF�ǶԶ��ǣ��ڡ�PGM����DNF���ۡ�BMN+��GHN��90�����ܡ�AMG+��CHG��270����������ȷ���۵ĸ����� ��
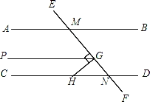
A.1��B.2 ��C.3��D.4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com