
【题目】如图,在直角坐标平面内,直线y=-x+5与 ![]() 轴和
轴和 ![]() 轴分别交于A、B两点,二次函数y=
轴分别交于A、B两点,二次函数y= ![]() +bx+c的图象经过点A、B,且顶点为C.
+bx+c的图象经过点A、B,且顶点为C.
(1)求这个二次函数的解析式;
(2)求sin∠OCA的值;
(3)若P是这个二次函数图象上位于x轴下方的一点,且 ![]() ABP的面积为10,求点P的坐标.
ABP的面积为10,求点P的坐标.
【答案】
(1)解:由直线y=-x+5得点B(0,5),A(5,0),将A、B两点的坐标代入 ![]() ,
,
得 ![]() ,解得
,解得 ![]() ∴抛物线的解析式为
∴抛物线的解析式为 ![]()
(2)解:过点C作CH⊥x轴交x轴于点H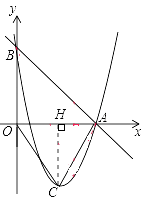
把 ![]() 配方得
配方得 ![]() ∴点C(3,-4),
∴点C(3,-4),
∴CH=4,AH=2,AC= ![]() ∴OC=5, ∵OA=5 ∴OA=OC ∴∠OAC=∠OCA
∴OC=5, ∵OA=5 ∴OA=OC ∴∠OAC=∠OCA
sin∠OCA=sin∠OAC= ![]()
(3)解:过P点作PQ ![]() x轴并延长交直线y=-x+5于Q
x轴并延长交直线y=-x+5于Q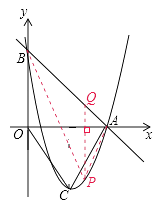
设点P(m, ![]() -6m+5),Q(m,-m+5) ∴PQ=-m+5-(
-6m+5),Q(m,-m+5) ∴PQ=-m+5-( ![]() -6m+5)=-
-6m+5)=- ![]() +5m
+5m
∵ ![]()
∴ ![]()
∴ ![]() ∴
∴ ![]()
∴P(1,0)(舍去),P(4,-3)
【解析】(1)根据直线y=-x+5与 ![]() 轴和
轴和 ![]() 轴分别交于A、B两点,求出A,B两点的坐标,然后将A、B两点的坐标代入
轴分别交于A、B两点,求出A,B两点的坐标,然后将A、B两点的坐标代入 ![]() ,得出关于c,b的方程组,解出方程组,求出c,b的值就能求出抛物线的解析式了;
,得出关于c,b的方程组,解出方程组,求出c,b的值就能求出抛物线的解析式了;
(2)过点C作CH⊥x轴交x轴于点H 将抛物线配方成顶点式,得出顶点C的坐标,从而得出CH,AH,的长,根据勾股定理得出AC,OC的长,进而判断出OA=OC 根据等边对等角得出∠OAC=∠OCA,然后根据等角的同名三角函数值相等得出答案;
(3)过P点作PQ ![]() x轴并延长交直线y=-x+5于Q,设点P(m, m 2 -6m+5),Q(m,-m+5) ∴PQ=-m+5-( m 2 -6m+5)=- m 2 +5m,根据
x轴并延长交直线y=-x+5于Q,设点P(m, m 2 -6m+5),Q(m,-m+5) ∴PQ=-m+5-( m 2 -6m+5)=- m 2 +5m,根据 ![]() 列出方程求解就能得出m的值,从而得出P点的坐标。
列出方程求解就能得出m的值,从而得出P点的坐标。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A、D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
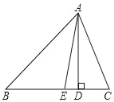
【题目】如图,在△ABC中,AD是BC边上的高,点E在BC上,AE是∠BAC的平分线,BE=AE,∠B=40°.
(1)求∠EAD的度数;
(2)求∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明是一个聪明而又富有想象力的孩子.学习了“有理数的乘方”后,他就琢磨着使用“乘方”这一数学知识脑洞大开地定义出“有理数的除方”概念.于是规定:若干个相同有理数(均不能为0)的除法运算叫做除方,如5÷5÷5,(﹣2)÷(﹣2)÷(﹣2)÷(﹣2)等,类比有理数的乘方.小明把5÷5÷5记作f(3,5),(﹣2)÷(﹣2)÷(﹣2)÷(﹣2)记作f(4,﹣2)
(1)直接写出计算结果,f(5,![]() )= ,f(6,3)= ;
)= ,f(6,3)= ;
(2)关于“有理数的除方”下列说法正确的是 (填序号)
①对于任何正整数n,都有f(n,﹣1)=1;
②f(6,3)=f(3,6);
③f(2,a)=1(a≠0);
④对于任何正整数n,都有f(2n,a)<0(a<0).
(3)小明深入思考后发现:“除方”运算能够转化成乘方运算,且结果可以写成幂的形式.请推导出“除方”的运算公式f(n,a)(n为正整数,a≠0,n≥2),要求写出推导过程将结果写成幂的形式(结果用含a,n的式子表示)
(4)请利用(3)问的推导公式计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.

(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com