
【题目】已知:如图,AB是⊙O的直径,AB=6,点C,D在⊙O上,且CD平分∠ACB,∠CAB=60°.
(1)求BC及阴影部分的面积;
(2)求CD的长.
【答案】
(1)解:∵AB是⊙O的直径,
∴∠ACB=90°.
在Rt△ACB中,
∵∠CAB=60°,AB=6,
∴BC=ABsin∠CAB=6× ![]() =3
=3 ![]() ,∠CBA=30°,
,∠CBA=30°,
如图1,连接OC,过点C作CE⊥x轴于点E, 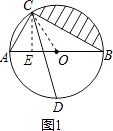
在Rt△BCE中,CE=BCsin∠CBA=3 ![]() ×
× ![]() ,
,
阴影部分的面积=S扇形OBC﹣S△OBC= ![]() ×π×9﹣
×π×9﹣ ![]() ×3=3π﹣
×3=3π﹣ ![]() ;
;
(2)解:连接AD, 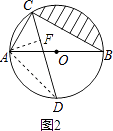
∵∠ABC=30°,
∴∠ADC=∠ABC=30°,
在△CAD中,AC=3,∠ACD=45°,
过点A作AF⊥CD于点F,在Rt△AFC中,AF=CF= ![]() ,
,
在Rt△AFD中,
∵DF= ![]() AF=
AF= ![]() ,
,
∴CD=CF+FD= ![]() +
+ ![]() .
.
【解析】(1)求阴影弓形的面积用扇形的面积减去三角形的面积。
(2)根据同弦所对的圆周角相等,构建有两个特殊角的三角形。CD平分∠ACB,所以有∠ACD=45°,然后作AF⊥CD,知AC边,求CD。
【考点精析】本题主要考查了圆周角定理和互余两角的三角函数关系的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;互余关系:sinA=cos(90°—A),cosA=sin(90°—A),tanA=cot(90°—A),cotA=tan(90°—A)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】(1)如图1,已知△ABC,BF平分外角∠CBP,CF平分外角∠BCQ.试确定∠A和∠F的数量关系;
(2)如图2,已知△ABC,BF和BD三等分外角∠CBP,CF和CE三等分外角∠BCQ.试确定∠A和∠F的数量关系;
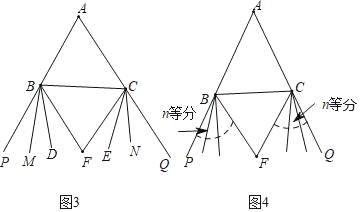
(3)如图3,已知△ABC,BF、BD和BM四等分外角∠CBP,CF、CE和CN四等分外角∠BCQ.试确定∠A和∠F的数量关系;
(4)如图4,已知△ABC,将外角∠CBP进行n等分,BF是临近BC边的等分线,将外角∠BCQ进行n等分,CF是临近BC边的等分线,试确定∠A和∠F的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】居民区内的“广场舞”引起媒体关注,辽宁都市频道为此进行过专访报道.小平想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A 非常赞同;B 赞同但要有时间限制;C 无所谓;D 不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.
请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)求图2中“C”层次所在扇形的圆心角的度数;
(4)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两支仪仗队各10名队员的身高(单位:cm)如下表:
甲队 | 179 | 177 | 178 | 177 | 178 | 178 | 179 | 179 | 177 | 178 |
乙队 | 178 | 178 | 176 | 180 | 180 | 178 | 176 | 179 | 177 | 178 |
(1)甲队队员的平均身高为cm,乙队队员的平均身高为cm;
(2)请用你学过的统计知识判断哪支仪仗队的身高更为整齐呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P点是灯塔所在位置,轮船A位于灯塔南偏东40°方向,轮船B位于灯塔北偏东30°方向,轮船C位于灯塔北偏西70°方向,航线PE(射线)平分∠BPC.
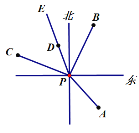
(1)求∠APE的度数;
(2)航线PE上的轮船D相对于灯塔P的方位是什么?
(以正北、正南方向为基准).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:y=kx+b(k≠0)与x轴、y轴分别交于A、B两点,与直线l2:y=3x交于点C,其中点C的坐标为(![]() ,c),点B的坐标为(0,3).
,c),点B的坐标为(0,3).
(1)求点C的坐标;
(2)求直线l1的表达式;
(3)在x轴上有一点D(3,0),求△BCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(x-2)(x-3)=m有实数根x1 , x2 , 且x1![]() x2有下列结论:①x1=2,x2=3;②m>
x2有下列结论:①x1=2,x2=3;②m> ![]() ;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中正确的结论是(填正确结论的序号)
;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中正确的结论是(填正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com