
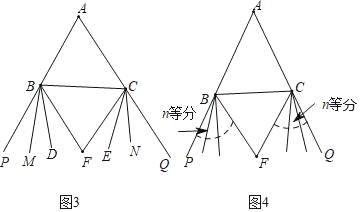
【题目】(1)如图1,已知△ABC,BF平分外角∠CBP,CF平分外角∠BCQ.试确定∠A和∠F的数量关系;
(2)如图2,已知△ABC,BF和BD三等分外角∠CBP,CF和CE三等分外角∠BCQ.试确定∠A和∠F的数量关系;
(3)如图3,已知△ABC,BF、BD和BM四等分外角∠CBP,CF、CE和CN四等分外角∠BCQ.试确定∠A和∠F的数量关系;
(4)如图4,已知△ABC,将外角∠CBP进行n等分,BF是临近BC边的等分线,将外角∠BCQ进行n等分,CF是临近BC边的等分线,试确定∠A和∠F的数量关系.

【答案】(1)∠F=90°-![]() ∠A,理由见解析;(2)∠F=120°-
∠A,理由见解析;(2)∠F=120°-![]() ∠A,理由见解析;(3) ∠F=135°-
∠A,理由见解析;(3) ∠F=135°-![]() ∠A,理由见解析;(4)∠F=
∠A,理由见解析;(4)∠F=![]() -
-![]() ∠A,理由见解析.
∠A,理由见解析.
【解析】
(1)利用三角形的外角的性质,角平分线的定义即可解决问题.
(2)利用三角形的外角的性质,三等分角的定义即可解决问题.
(3)利用三角形的外角的性质,四等分角的定义即可解决问题.
(4)利用三角形的外角的性质,n等分角的定义即可解决问题.
(1)由已知得∠CBF=![]() ∠CBP,∠BCF=
∠CBP,∠BCF=![]() ∠BCQ,
∠BCQ,
∵∠CBP=∠A+∠ACB,∠BCQ=∠A+∠ABC,
∴∠CBF+∠BCF=![]() (∠A+∠ACB+∠A+ABC)=
(∠A+∠ACB+∠A+ABC)=![]() (∠A+1800),
(∠A+1800),
∠F=1800-(∠CBF+∠BCF)=1800-![]() (∠A+1800)= 90°-
(∠A+1800)= 90°-![]() ∠A;
∠A;
(2)由已知得∠CBF=![]() ∠CBP,∠BCF=
∠CBP,∠BCF=![]() ∠BCQ,
∠BCQ,
∵∠CBP=∠A+∠ACB,∠BCQ=∠A+∠ABC,
∴∠CBF+∠BCF=![]() (∠A+∠ACB+∠A+ABC)=
(∠A+∠ACB+∠A+ABC)=![]() (∠A+1800),
(∠A+1800),
∠F=1800-(∠CBF+∠BCF)=1800-![]() (∠A+1800)= 120°-
(∠A+1800)= 120°-![]() ∠A;
∠A;
(3)由已知得∠CBF=![]() ∠CBP,∠BCF=
∠CBP,∠BCF=![]() ∠BCQ,
∠BCQ,
∵∠CBP=∠A+∠ACB,∠BCQ=∠A+∠ABC,
∴∠CBF+∠BCF=![]() (∠A+∠ACB+∠A+ABC)=
(∠A+∠ACB+∠A+ABC)=![]() (∠A+1800),
(∠A+1800),
∠F=1800-(∠CBF+∠BCF)=1800-![]() (∠A+1800)= 135°-
(∠A+1800)= 135°-![]() ∠A;
∠A;
(4)由已知得∠CBF=![]() ∠CBP,∠BCF=
∠CBP,∠BCF=![]() ∠BCQ,
∠BCQ,
∴∠CBP=∠A+∠ACB,∠BCQ=∠A+∠ABC,
∴∠CBF+∠BCF=![]() (∠A+∠ACB+∠A+ABC)=
(∠A+∠ACB+∠A+ABC)=![]() (∠A+1800),
(∠A+1800),
∠F=1800-(∠CBF+∠BCF)=1800-![]() (∠A+1800)=
(∠A+1800)=![]() 180°-
180°-![]() ∠A.
∠A.


科目:初中数学 来源: 题型:
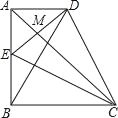
【题目】如图,四边形ABCD中,∠DAB=∠ABC=90°,AB=BC,E是AB的中点,CE⊥BD.
(1)求证:BE=AD;
(2)求证:AC是线段ED的垂直平分线;
(3)△DBC是等腰三角形吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两汽车,甲从A地去B地,乙从B地去A地,同时相向而行,1.5小时后两车相遇.相遇后,甲车还需要2小时到达B地,乙车还需要![]() 小时到达A地.若A、B两地相距210千米,试求甲乙两车的速度.
小时到达A地.若A、B两地相距210千米,试求甲乙两车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
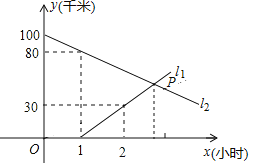
【题目】A,B两地相距100千米,甲,乙两人骑车分别从A,B两地相向而行,图中![]() 和
和![]() 分别表示他们各自到A地的距离
分别表示他们各自到A地的距离![]() 千米
千米![]() 与时间
与时间![]() 小时
小时![]() 的关系,根据图中提供的信息,解答下列问题:
的关系,根据图中提供的信息,解答下列问题:
![]() 图中哪条线表示甲到A地的距离与时间的关系?
图中哪条线表示甲到A地的距离与时间的关系?
![]() 甲,乙两人的速度分别是多少?
甲,乙两人的速度分别是多少?
![]() 求P点的坐标,并解释P点的实际意义.
求P点的坐标,并解释P点的实际意义.
![]() 甲出发多长时间后,两人相距30千米?
甲出发多长时间后,两人相距30千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是以点O为圆心,AB为直径的半圆上的动点(点C不与点A,B重合),AB=4.设弦AC的长为x,△ABC的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )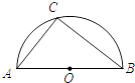
A.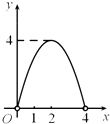
B.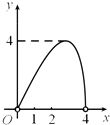
C.
D.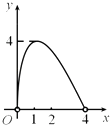
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.
(1)这50名同学捐款的众数为元,中位数为元;
(2)求这50名同学捐款的平均数;
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段![]() 、
、![]() 、
、![]() ;
;
求作:△ABC,使![]() ,
, ![]() ,
, ![]() ;
;

【答案】答案见解析
【解析】试题分析:先画出与![]() 相等的角,再画出
相等的角,再画出![]() 的长,连接
的长,连接![]() ,则
,则![]() 即为所求三角形.
即为所求三角形.
试题解析:如图所示:①先画射线BC,
②以α的顶点为圆心,任意长为半径画弧,分别交α的两边交于为A′,C′;
③以相同长度为半径,B为圆心,画弧,交BC于点F,以F为圆心,C′A′为半径画弧,交于点E;
④在BF上取点C,使CB=a,以B为圆心,c为半径画圆交BE的延长线于点A,连接AC,
结论:△ABC即为所求三角形.

【题型】解答题
【结束】
15
【题目】已知:线段![]() ,
, ![]() ,求作:
,求作: ![]() ,使
,使![]() ,
, ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,AB=6,点C,D在⊙O上,且CD平分∠ACB,∠CAB=60°.
(1)求BC及阴影部分的面积;
(2)求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com