
【题目】甲、乙两汽车,甲从A地去B地,乙从B地去A地,同时相向而行,1.5小时后两车相遇.相遇后,甲车还需要2小时到达B地,乙车还需要![]() 小时到达A地.若A、B两地相距210千米,试求甲乙两车的速度.
小时到达A地.若A、B两地相距210千米,试求甲乙两车的速度.
 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 2000 |
频率 | 0.365 | 0.328 | 0.330 | 0.334 | 0.336 | 0.332 | 0.333 |
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.抛一个质地均匀的正六面体骰子,向上的面点数是5
D.抛一枚硬币,出现反面的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,AF=4,CF=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有2个红球(记为红球1、红球2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是;
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表),求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B在数轴上分别表示a、b
(1)对照数轴填写下表:
a | 6 | -6 | -6 | -6 | -10 | -2.5 |
b | 4 | 0 | 4 | -4 | 2 | -2.5 |
两点距离 | 2 | 6 | 0 |
(2)若A、B两点间的距离记为 d,试问d与a、b有何数量关系;
(3)在数轴上找到所有符合条件的整数点P,使它到5和﹣5的距离之和为10,并求出所有这些整数的和;
(4)若数轴上点C表示的数为x,当点C在什么位置时,
①|x+1|的值最小;②|x+1|+|x﹣2|的值最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
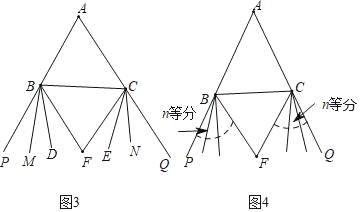
【题目】(1)如图1,已知△ABC,BF平分外角∠CBP,CF平分外角∠BCQ.试确定∠A和∠F的数量关系;
(2)如图2,已知△ABC,BF和BD三等分外角∠CBP,CF和CE三等分外角∠BCQ.试确定∠A和∠F的数量关系;
(3)如图3,已知△ABC,BF、BD和BM四等分外角∠CBP,CF、CE和CN四等分外角∠BCQ.试确定∠A和∠F的数量关系;
(4)如图4,已知△ABC,将外角∠CBP进行n等分,BF是临近BC边的等分线,将外角∠BCQ进行n等分,CF是临近BC边的等分线,试确定∠A和∠F的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】居民区内的“广场舞”引起媒体关注,辽宁都市频道为此进行过专访报道.小平想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A 非常赞同;B 赞同但要有时间限制;C 无所谓;D 不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.
请你根据图中提供的信息解答下列问题:
(1)求本次被抽查的居民有多少人?
(2)将图1和图2补充完整;
(3)求图2中“C”层次所在扇形的圆心角的度数;
(4)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com