
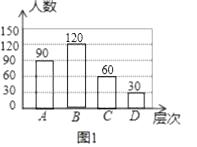
����Ŀ���������ڵġ��㳡�衱����ý���ע����������Ƶ��Ϊ�˽��й�ר�ñ�����Сƽ���˽ⱾС������ԡ��㳡�衱�Ŀ�����������һ�γ������飬�Ѿ���ԡ��㳡�衱�Ŀ�����Ϊ�ĸ���Σ�A �dz���ͬ��B ��ͬ��Ҫ��ʱ�����ƣ�C ����ν��D ����ͬ������������������ͼ1��ͼ2������������ͳ��ͼ��
�������ͼ���ṩ����Ϣ����������⣺
��1���α����ľ����ж����ˣ�
��2����ͼ1��ͼ2����������
��3����ͼ2�С�C������������ε�Բ�ĽǵĶ�����
��4�����Ƹ�С��4000�������жԡ��㳡�衱�Ŀ�����ʾ��ͬ������A��κ�B��Σ��Ĵ�Լ�ж����ˣ�
���𰸡�
��1���⣺��90��30%=300���ˣ���
�౾�α����ľ�����300�ˣ�
��2���⣺��D��ռ�İٷֱȣ�30��300=10%��
��B��ռ�İٷֱȣ�1��20%��30%��10%=40%��
��B��Ӧ��������300��40%=120���ˣ���C��Ӧ��������300��20%=60���ˣ���
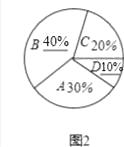
��3���⣺��C������������ε�Բ�ĽǵĶ�����360![]()
![]() 20%=72
20%=72![]()
��4���⣺��4000����30%+40%��=2800���ˣ���
����Ƹ�С��4000�������жԡ��㳡�衱�Ŀ�����ʾ��ͬ������A��κ�B��Σ��Ĵ�Լ��2800�ˣ�
����������1�����α����ľ���=�dz���ͬ������![]() �dz���ͬ��������ռ�İٷֱȼ��ɣ�
�dz���ͬ��������ռ�İٷֱȼ��ɣ�
��2��D����ռ�İٷֱ�=D�������![]() ���α����ľ������������B��ռ�İٷֱ�=1-C��ռ�İٷֱ�-D��ռ�İٷֱ�-A��ռ�İٷֱ�; B��Ӧ������=���α����ľ����������
���α����ľ������������B��ռ�İٷֱ�=1-C��ռ�İٷֱ�-D��ռ�İٷֱ�-A��ռ�İٷֱ�; B��Ӧ������=���α����ľ����������![]() B��ռ�İٷֱ�; C��Ӧ������=���α����ľ����������
B��ռ�İٷֱ�; C��Ӧ������=���α����ľ����������![]() C��ռ�İٷֱ�;���ݼ�������ݲ�ȫ��ͳ��ͼ��
C��ռ�İٷֱ�;���ݼ�������ݲ�ȫ��ͳ��ͼ��
��3����C������������ε�Բ�ĽǵĶ���=360![]()
![]() C��ռ�İٷֱȼ��ɣ�
C��ռ�İٷֱȼ��ɣ�
��4����С��4000�������жԡ��㳡�衱�Ŀ�����ʾ��ͬ������A��κ�B��Σ�������=4000![]() ��A��ռ�İٷֱ�+B��ռ�İٷֱȣ����ɡ�
��A��ռ�İٷֱ�+B��ռ�İٷֱȣ����ɡ�
�����㾫����������Ҫ����������ͳ��ͼ������ͳ��ͼ�����֪ʶ�㣬��Ҫ����������ر�ʾ������������������ռ�İٷֱȣ����Dz�������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�Լ�����ı仯�����������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�����Dz�������ر�ʾ��������������������ռ�İٷֱ��Լ�����ı仯���������ȷ�����⣮


 �ο�������ϵ�д�
�ο�������ϵ�д� ������ѧ��ʱ��ҵϵ�д�
������ѧ��ʱ��ҵϵ�д� ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������������״�A��ȥB�أ��Ҵ�B��ȥA�أ�ͬʱ������У�1.5Сʱ�����������������׳�����Ҫ2Сʱ����B�أ��ҳ�����Ҫ![]() Сʱ����A�أ���A��B�������210ǧ�ף���������������ٶȣ�
Сʱ����A�أ���A��B�������210ǧ�ף���������������ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���߶�![]() ��
��![]() ��
��![]() ��
��
��������ABC��ʹ![]() ��
�� ![]() ��
�� ![]() ��
��

���𰸡��𰸼�����
������������������Ȼ�����![]() ��ȵĽǣ��ٻ���
��ȵĽǣ��ٻ���![]() �ij�������
�ij�������![]() ����
����![]() ������������
������������
�����������ͼ��ʾ�����Ȼ�����BC��
�������Ķ���ΪԲ��,���ⳤΪ�뾶����,�ֱ��������߽���ΪA��,C����
������ͬ����Ϊ�뾶,BΪԲ��,����,��BC�ڵ�F,��FΪԲ��,C��A��Ϊ�뾶���������ڵ�E��
����BF��ȡ��C��ʹCB=a����BΪԲ�ģ�cΪ�뾶��Բ��BE���ӳ����ڵ�A������AC��
���ۣ���ABC��Ϊ����������.

�����͡������
��������
15
����Ŀ����֪���߶�![]() ��
�� ![]() ��������
�������� ![]() ��ʹ
��ʹ![]() ��
�� ![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ABΪ��O��ֱ��AC��ADΪ��O���ң���AB=2AC= ![]() AD�����DBC�Ķ���Ϊ ��
AD�����DBC�Ķ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() Ϊ��
��![]() ��
��![]() ��
��![]() ��ƽ���ߵĽ��㣬�ֱ����
��ƽ���ߵĽ��㣬�ֱ����![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() �㣬���ܹ����
�㣬���ܹ����![]() �Ķ�����������д�������̣�
�Ķ�����������д�������̣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
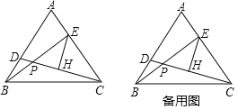
����Ŀ����ͼ���ڵȱ���ABC�У���D����E�ֱ���AB��AC�ϣ�BD=AE������BE��CD���ڵ�P����EH��CD��H��
��1����֤����CAD�ա�BCE����2����֤��PE=2PH����3����PB=PH�����ACD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
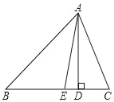
����Ŀ����ͼ���ڡ�ABC�У�AD��BC���ϵĸߣ���E��BC�ϣ�AE�ǡ�BAC��ƽ���ߣ�BE��AE����B��40����
��1�����EAD�Ķ�����
��2�����C�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��AB�ǡ�O��ֱ����AB=6����C��D�ڡ�O�ϣ���CDƽ�֡�ACB����CAB=60�㣮
��1����BC����Ӱ���ֵ������
��2����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�����A��AE��BC������ΪE������DE��FΪ�߶�DE��һ�㣬�ҡ�AFE����B��
��1����֤����ADF�ס�DEC
��2����AB��4��AD��3 ![]() ��AE��3����AF�ij���
��AE��3����AF�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com