[题目]已知AB为⊙O的直径AC.AD为⊙O的弦.若AB=2AC= AD.则∠DBC的度数为．题目和参考答案——青夏教育精英家教网—

【题目】已知AB为⊙O的直径AC、AD为⊙O的弦，若AB=2AC= AD，则∠DBC的度数为．

【答案】15°或75°
【解析】本题需要分两种情况进行讨论，根据题意可得：∠ACB=∠ADB=90°，根据弦长之间的关系可得：∠ABC=30°，∠ABD=45°，当AC和AD在AB的异侧时，∠DBC=30°+45°=75°；当AC和AD在AB同侧时，∠DBC=45°－30°=15°．
【考点精析】关于本题考查的等腰直角三角形和含30度角的直角三角形，需要了解等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半才能得出正确答案．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，⊙O的直径AC与弦BD相交于点F，点E是DB延长线上一点，∠EAB＝∠ADB.

（1）求证：EA是⊙O的切线；
（2）已知点B是EF的中点，AF＝4，CF＝2，求AE的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

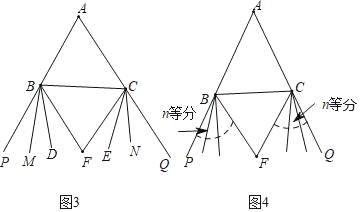
【题目】（1）如图1，已知△ABC，BF平分外角∠CBP，CF平分外角∠BCQ．试确定∠A和∠F的数量关系；

（2）如图2，已知△ABC，BF和BD三等分外角∠CBP，CF和CE三等分外角∠BCQ．试确定∠A和∠F的数量关系；

（3）如图3，已知△ABC，BF、BD和BM四等分外角∠CBP，CF、CE和CN四等分外角∠BCQ．试确定∠A和∠F的数量关系；

（4）如图4，已知△ABC，将外角∠CBP进行n等分，BF是临近BC边的等分线，将外角∠BCQ进行n等分，CF是临近BC边的等分线，试确定∠A和∠F的数量关系．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】（知识生成）我们知道，用两种不同的方法计算同一个几何图形的面积，可以得到一些代数恒等式.

例如：如图可以得到(a+b)2=a2+2ab+b2，基于此，请解答下列问题：

⑴ 根据如图，写出一个代数恒等式：

；

⑵ 利用⑴中得到的结论，解决下面的问题：若a+b+c=12，，

则；

⑶ 小明同学用如图中x张边长为a的正方形，y张边长为b的正方形，z张宽、长分别为a、b的长方形纸片拼出一个面积为(2a+b)(a+3b)的长方形，则x＋y＋z= ；

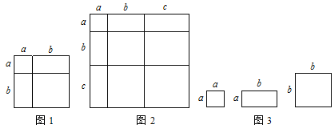
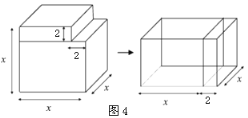
（知识迁移）⑷ 类似地，用两种不同的方法计算几何体的体积同样可以得到一些代数恒等式．如图表示的是一个边长为x的正方体挖去一个边长为2的小长方体后重新拼成一个新长方体．请你根据如图中两个图形的变化关系，写出一个代数恒等式．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，二次函数y=ax2+bx+c的图象经过（-1，0）（0，3），下列结论中错误的是（）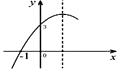

A.abc＜0
B.9a+3b+c=0
C.a-b=-3
D.4ac﹣b2＜0

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图所示，，结论：①；②；③；④，其中正确的是有（）

A.1个B.2个C.3个D.4个

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】居民区内的“广场舞”引起媒体关注，辽宁都市频道为此进行过专访报道．小平想了解本小区居民对“广场舞”的看法，进行了一次抽样调查，把居民对“广场舞”的看法分为四个层次：A 非常赞同；B 赞同但要有时间限制；C 无所谓；D 不赞同．并将调查结果绘制了图1和图2两幅不完整的统计图．

请你根据图中提供的信息解答下列问题：
（1）求本次被抽查的居民有多少人？
（2）将图1和图2补充完整；
（3）求图2中“C”层次所在扇形的圆心角的度数；
（4）估计该小区4000名居民中对“广场舞”的看法表示赞同（包括A层次和B层次）的大约有多少人．