
����Ŀ�����г���ij�ܼƻ�����2100���綯����ƽ��ÿ�������綯��300�������ڸ���ԭ��ʵ��ÿ�����������ƻ�ÿ�������������г��룬�±��Ǹ��ܵ�ʵ���������(������Ϊ����������Ϊ������λ����)��
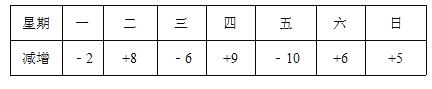
��1���ó�����һ�����綯���������� ����
��2������������һ������������ٵ�һ��������綯���������� ����
��3���ó�ʵ�мǼ������ƣ�ÿ����һ�����ɵ�60Ԫ����ô�ó�������һ�ܵĹ����ܶ��Ƕ���Ԫ��
���𰸡���1��298����2��19����3���ó�������һ�ܵĹ����ܶ���126600Ԫ��
��������
��1�����������üƻ�ƽ��ÿ�����������ϼ���������.
��2�����ݱ������ݣ�����������һ��Ϊ300+9=309�������ٵ�һ��Ϊ300��10=290����ǰ��ȥ������.
��3��ֱ�ӽ�ͼ��������������ӿɵ�һ��������������������,���ϼƻ�������,�ٳ��Ե������ʼ��ɽ��.
��:��1����ÿ��ƽ��300����������Ϊ����������Ϊ��������һ�����糵Ϊ300��2=298��
��2��������������һ��Ϊ300+9=309�������������ٵ�һ��Ϊ300��10=290����309-290=19��
������������һ������������ٵ�һ��������綯��19����
��3��һ���ܹ������糵Ϊ7��300+(��2+8��6+9��10+6+5)=2110����
��ó�������һ�ܵĹ����ܶ���60��2110=126600Ԫ��
�𣺸ó�������һ�ܵĹ����ܶ���126600Ԫ��
�ʴ�Ϊ��298��19, 126600.


 �ظ���ʦ�㲦ϵ�д�
�ظ���ʦ�㲦ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
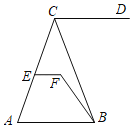
����Ŀ����ͼ��EF��AB����DCB��65������CBF��15������EFB��130����
��1��ֱ��CD��ABƽ����Ϊʲô��
��2������CEF��68�������ACB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��ABC�ı�BC��x���ϣ�A��C���������ֱ�ΪA��0��m����C��n��0����B����5��0�����ң�n��3��2+![]() =0��һ����P�ӵ�B��������ÿ��2��λ���ȵ��ٶ�������BO�����˶������P�˶���ʱ��Ϊts��
=0��һ����P�ӵ�B��������ÿ��2��λ���ȵ��ٶ�������BO�����˶������P�˶���ʱ��Ϊts��
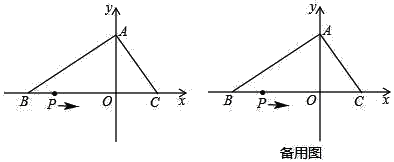
��1����A��C��������ꣻ
��2������PA������PABΪ���������Σ����P�����ꣻ
��3������P���߶�BO���˶�ʱ����y�����Ƿ���ڵ�Q��ʹ��POQ����AOCȫ�ȣ������ڣ������t��ֵ��ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���![]() ��ͼ����x�ύ��A��B���㣬B�������Ϊ(3��0)����y�ύ�ڵ�C��0����3������P��ֱ��BC�·��������ϵ�һ�����㣮
��ͼ����x�ύ��A��B���㣬B�������Ϊ(3��0)����y�ύ�ڵ�C��0����3������P��ֱ��BC�·��������ϵ�һ�����㣮
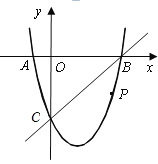
��1������κ�������ʽ��
��2������PO��PC��������POC��y����ۣ��õ��ı���![]() .�Ƿ���ڵ�P��ʹ�ı���
.�Ƿ���ڵ�P��ʹ�ı���![]() Ϊ���Σ������ڣ������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
Ϊ���Σ������ڣ������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
��3������P�˶���ʲôλ��ʱ���ı���ABPC�������������ʱP���������ı���ABPC��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������ڱ�ֱ�Ĺ�·��ͬ��㡢ͬ����ͬ�յ�������ʻ![]() ���ȵ��յ����ԭ����Ϣ.��֪���ȳ���
���ȵ��յ����ԭ����Ϣ.��֪���ȳ���![]() �������������У��ס��������ľ���
�������������У��ס��������ľ���![]() ��׳�����ʱ��
��׳�����ʱ��![]() ֮��Ĺ�ϵ��ͼ��ʾ.
֮��Ĺ�ϵ��ͼ��ʾ.
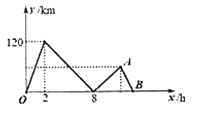
��1�����ٶ�Ϊ______![]() ���ҵ��ٶ�Ϊ______
���ҵ��ٶ�Ϊ______![]() ��
��
��2��˵��![]() ���ʾ�����壬���
���ʾ�����壬���![]() �����ꣻ
�����ꣻ
��3������߶�![]() �ĺ�����ϵʽ����д��
�ĺ�����ϵʽ����д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��4���׳����ʱ���������![]() ��ֱ��д�����.
��ֱ��д�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ѧ��ҵ�ؼ��紴ҵ����һ����ֲ�辰�뻨�ܸ�50���ۺ�ͳ�����辰��ƽ��ÿ��������160Ԫ�����ܵ�ƽ��ÿ��������19Ԫ�����з��֣�
���辰ÿ����1�����辰��ƽ��ÿ���������2Ԫ;ÿ����1�����辰��ƽ��ÿ����������2Ԫ;�ڻ��ܵ�ƽ��ÿ������ʼ�ղ���.
С���ƻ��ڶ�����ֲ�辰�뻨�ܹ�100��������ֲ���辰�ȵ�һ������x�����ڶ����辰�뻨������������ֱ�ΪW1��W2����λ��Ԫ��
��1���ú�x�Ĵ���ʽ�ֱ��ʾW1��W2;
��2����xȡ��ֵʱ���ڶ�����ֲ���辰�뻨��������õ�������W���������������Ƕ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������С�����εı߳���Ϊ 1��A��B��C ���ڸ���ϣ�С�����εĶ��������㣩�������û�п̶ȵ�ֱ����ɻ�ͼ����Ҫ��д�����������
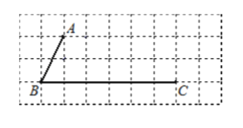
��1������C��ֱ��AB��ƽ����CD��
��2������A��ֱ��BC�Ĵ��ߣ���ע������ΪG������A��ֱ��AB�Ĵ��ߣ���BC�ڵ�H��
��3���߶� �ij����ǵ� A ��ֱ�� BC �ľ��룻
��4����B���HAG�Ĵ�С��ϵΪ �������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
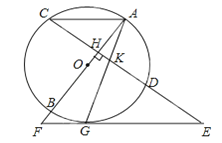
����Ŀ����ͼ��AB�ǡ�O��ֱ������CD��AB��H����CD�ӳ�����һ��E����O�����߽�AB���ӳ������е�ΪG������AG��CD��K��
��1����֤��KE=GE��
��2����KG2=KDGE�����ж�AC��EF��λ�ù�ϵ����˵�����ɣ�
��3���ڣ�2���������£���sinE=![]() ��AK=
��AK=![]() ����FG�ij���
����FG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
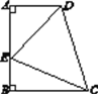
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����A����B��90�㣬AB��5![]() ����E��AB�ϣ���AED��45�㣬DE��6��CE��7.��AE�ij���sin��BCE��ֵ��
����E��AB�ϣ���AED��45�㣬DE��6��CE��7.��AE�ij���sin��BCE��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com