
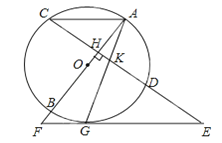
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于切点为G,连接AG交CD于K.
(1)求证:KE=GE;
(2)若KG2=KDGE,试判断AC与EF的位置关系,并说明理由;
(3)在(2)的条件下,若sinE=![]() ,AK=
,AK=![]() ,求FG的长.
,求FG的长.
【答案】(1)证明见解析;(2)AC∥EF,证明见解析;(3)FG= ![]() .
.
【解析】
试题(1)如图1,连接OG.根据切线性质及CD⊥AB,可以推出∠KGE=∠AKH=∠GKE,根据等角对等边得到KE=GE;
(2)AC与EF平行,理由为:如图2所示,连接GD,由∠KGE=∠GKE,及KG2=KDGE,利用两边对应成比例且夹角相等的两三角形相似可得出△GKD与△EKG相似,又利用同弧所对的圆周角相等得到∠C=∠AGD,可推知∠E=∠C,从而得到AC∥EF;
(3)如图3所示,连接OG,OC,先求出KE=GE,再求出圆的半径,根据勾股定理与垂径定理可以求解;然后在Rt△OGF中,解直角三角形即可求得FG的长度.
试题解析:(1)如图1,连接OG.
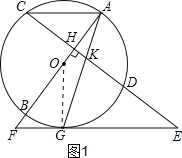
∵EG为切线,
∴∠KGE+∠OGA=90°,
∵CD⊥AB,
∴∠AKH+∠OAG=90°,
又∵OA=OG,
∴∠OGA=∠OAG,
∴∠KGE=∠AKH=∠GKE,
∴KE=GE.
(2)AC∥EF,理由为连接GD,如图2所示.
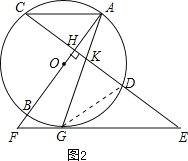
∵KG2=KDGE,即![]() ,
,
∴![]() ,
,
又∵∠KGE=∠GKE,
∴△GKD∽△EGK,
∴∠E=∠AGD,
又∵∠C=∠AGD,
∴∠E=∠C,
∴AC∥EF;
(3)连接OG,OC,如图3所示,
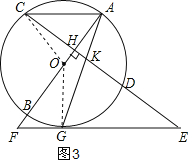
∵EG为切线,
∴∠KGE+∠OGA=90°,
∵CD⊥AB,
∴∠AKH+∠OAG=90°,
又∵OA=OG,
∴∠OGA=∠OAG,
∴∠KGE=∠AKH=∠GKE,
∴KE=GE.
∵sinE=sin∠ACH=![]()
,设AH=3t,则AC=5t,CH=4t,
∵KE=GE,AC∥EF,
∴CK=AC=5t,
∴HK=CK-CH=t.
在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,
即(3t)2+t2=(2![]() )2,解得t=
)2,解得t=![]() .
.
设⊙O半径为r,在Rt△OCH中,OC=r,OH=r-3t,CH=4t,
由勾股定理得:OH2+CH2=OC2,
即(r-3t)2+(4t)2=r2,解得r=![]() t=
t=![]() .
.
∵EF为切线,
∴△OGF为直角三角形,
在Rt△OGF中,OG=r=![]() ,tan∠OFG=tan∠CAH=
,tan∠OFG=tan∠CAH=![]() ,
,
∴FG=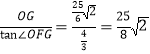


科目:初中数学 来源: 题型:
【题目】把一个足球垂直水平地面向上踢,时间为t(秒)时该足球距离地面的高度h(米)适用公式h=20t﹣5t2(0≤t≤4).
(1)当t=3时,求足球距离地面的高度;
(2)当足球距离地面的高度为10米时,求t;
(3)若存在实数t1,t2(t1≠t2)当t=t1或t2时,足球距离地面的高度都为m(米),求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自行车厂某周计划生产2100辆电动车,平均每天生产电动车300辆.由于各种原因,实际每天的生产量与计划每天的生产量相比有出入,下表是该周的实际生产情况(超产记为正、减产记为负,单位:辆):
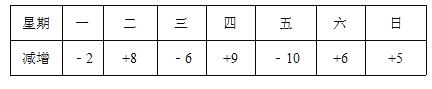
(1)该厂星期一生产电动车 辆;
(2)生产量最多的一天比生产量最少的一天多生产电动车 辆;
(3)该厂实行记件工资制,每生产一辆车可得60元,那么该厂工人这一周的工资总额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具厂生产一种课桌和椅子,课桌每张定价200 元,椅子每把定价80元,厂方在开展促销活动期间,向客户提供两种优惠方案:方案一:每买一张课桌就赠送一把椅子;方案二:课桌和椅子都按定价的80%付款.某校计划添置100张课桌和x把椅子.
(1)若x>100,请用含x的代数式分别把两种方案的费用表示出来;
(2)若x=300,如果两种方案可以同时使用,作为一种新的方案,请帮助学校设计一种最省钱的方案
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与探究:已知:点O为直线AB上一点,∠COD=90°,射线OE平分∠AOD.
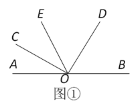
(1)如图①所示,若∠COE=20°,则∠BOD= °.
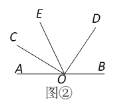
(2)若将∠COD绕点O旋转至图②的位置,试判断∠BOD和∠COE的数量关系,并说明理由;
(3)若将∠COD绕点O旋转至图③的位置,继续探究∠BOD和∠COE的数量关系,请直接写出∠BOD和∠COE之间的数量关系: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC外切于⊙O,切点分别为点D,E,F,∠A=60°,BC=7,⊙O的半径为![]() .求:(1)求BF+CE的值; (2)求△ABC的周长.
.求:(1)求BF+CE的值; (2)求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若干个完全相同的小正方体堆成一个几何体.
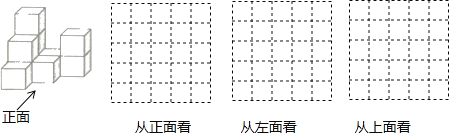
(1)从正面、左面、上面观察该几何体,分别在所给的网格图中画出你所看到的形状图;
(2)若现在你手头还有一些相同的小正方体,如果保持从左面、上面观察该几何体得到的形状图不变,那么在这个几何体上最多可以再添加多少个小正方体?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(x-1)(x+1)=x2-1,
(x-1)(x2+x+1)=x3-1,
(x-1)(x3+x2+x+1)=x4-1,
(x-1)(x4+x3+x2+x+1)= ,
………
猜想:(x-1)(xn+xn-1+…+x2+x+1)= ,
(2)根据以上结果,试写出下面两式的结果
①(x-1)(x49+x48+…+x2+x+1)= ,
②(x20-1)÷(x-1)= ,
(3)利用以上结论求值:1+3+32+33+34+……+32018
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com