
【题目】操作与探究:已知:点O为直线AB上一点,∠COD=90°,射线OE平分∠AOD.
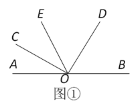
(1)如图①所示,若∠COE=20°,则∠BOD= °.
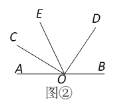
(2)若将∠COD绕点O旋转至图②的位置,试判断∠BOD和∠COE的数量关系,并说明理由;
(3)若将∠COD绕点O旋转至图③的位置,继续探究∠BOD和∠COE的数量关系,请直接写出∠BOD和∠COE之间的数量关系: .

【答案】(1)40°;(2)∠BOD=2∠COE,理由见详解;(3)∠BOD+2∠COE=360°,理由见详解
【解析】
(1)由互余得∠DOE的度数,进而由角平分线得出∠AOE的度数,即可得出∠BOD的度数;
(2)由互余及角平分线得∠DOE=90°-∠COE=∠AOE,∠AOC=∠AOE-∠COE=90°-2∠COE,最后根据∠BOD=180°-∠AOC-∠COD可得;
(3)由互余得∠DOE=∠COE-90°,由角平分线得∠AOD=2∠DOE=2∠COE-180°,最后根据∠BOD=180°-∠AOD可得.
解:(1)![]()
∵射线OE平分∠AOD
∴![]()
∴![]() ;
;
(2)![]() ,理由如下:
,理由如下:
∵∠COD=90°
∴∠DOE=∠COE-90°
∵射线OE平分∠AOD
∴∠AOC=∠AOE-∠COE=90°-2∠COE
∵A,O,B在同一直线上
∴∠BOD=180°-∠AOC-∠COD=180°-(90°-2∠COE)- 90°
即:∠BOD=2∠COE;
(3)∠BOD+2∠COE=360°,理由如下:
∵∠COD=90°
∴∠DOE=∠COE-90°
∵射线OE平分∠AOD
∴∠AOD=2∠DOE=2∠COE-180°
∴∠BOD=180°-∠AOD=360°-2∠COE
即:∠BOD+2∠COE=360°.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两车在笔直的公路上同起点、同方向、同终点匀速行驶![]() ,先到终点的人原地休息.已知甲先出发
,先到终点的人原地休息.已知甲先出发![]() ,在整个过程中,甲、乙两车的距离
,在整个过程中,甲、乙两车的距离![]() 与甲出发的时间
与甲出发的时间![]() 之间的关系如图所示.
之间的关系如图所示.
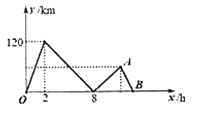
(1)甲的速度为______![]() ,乙的速度为______
,乙的速度为______![]() ;
;
(2)说明![]() 点表示的意义,求出
点表示的意义,求出![]() 点坐标;
点坐标;
(3)求出线段![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(4)甲出发多长时间两车相距![]() ,直接写出结果.
,直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有小正方形的边长都为 1,A、B、C 都在格点上(小正方形的顶点叫做格点).请仅用没有刻度的直尺完成画图(不要求写画法)及解答:
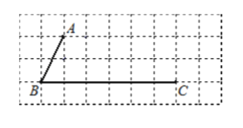
(1)过点C画直线AB的平行线CD;
(2)过点A画直线BC的垂线,并注明垂足为G;过点A画直线AB的垂线,交BC于点H;
(3)线段 的长度是点 A 到直线 BC 的距离;
(4)∠B与∠HAG的大小关系为 ,理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
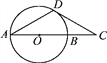
【题目】如图所示,D是半径为R的⊙O上一点,过点D作⊙O的切线交直径AB的延长线于点C,下列四个条件:①AD=CD;②∠A=30°;③∠ADC=120°;④DC=![]() R.其中能使得BC=R的有________(填序号).
R.其中能使得BC=R的有________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
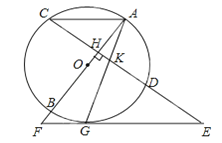
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于切点为G,连接AG交CD于K.
(1)求证:KE=GE;
(2)若KG2=KDGE,试判断AC与EF的位置关系,并说明理由;
(3)在(2)的条件下,若sinE=![]() ,AK=
,AK=![]() ,求FG的长.
,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
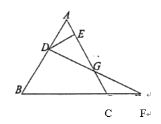
【题目】如图,在边长为1的等边△ABC的边AB取一点D,过点D作DE⊥AC于点E,在BC延长线取一点F,使CF=AD,连接DF交AC于点G,则EG的长为________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过点A作AE//BC与过点D作CD的垂线交于点E.
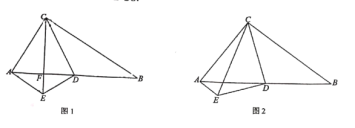
(1)如图1,若CE交AD于点F,BC=6,∠B=30°,求AE的长
(2)如图2,求证AE+CE=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高节水意识,小申随机统计了自己家7天的用水量,并分析了第3天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.(单位:升)
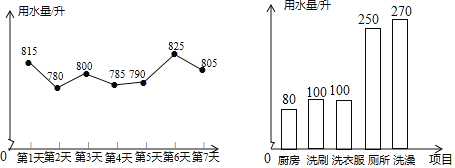
(1)求这7天内小申家每天用水量的平均数和中位数;
(2)求第3天小申家洗衣服的水占这一天总用水量的百分比;
(3)若规定居民生活用水收费标准为2.80元/立方米,请你估算小申家一个月(按30天计算)的水费是多少元?(1立方米=1000升)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com