【题目】小明家客厅里装有一种三位单极开关，分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯，按下任意一个开关均可打开对应的一盏电灯，因刚搬进新房不久，不熟悉情况．
（1）若小明任意按下一个开关，则小明打开走廊灯的概率是多少？
（2）若任意按下一个开关后，再按下另两个开关中的一个，则正好客厅灯和走廊灯同时亮的概率是多少？请用树状图法或列表法加以说明．
华东师大版一课一练系列答案科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，△ABC的边BC在x轴上，顶点A在y轴的正半轴上，OA=2，OB=1，OC=4．
（1）求过A、B、C三点的抛物线的解析式；
（2）设点M是x轴上的动点，试问：在平面直角坐标系中，是否存在点N，使得以点A，B，M，N为顶点的四边形是菱形？若存在，直接写出点N的坐标；若不存在，说明理由；
（3）若抛物线对称轴交x轴于点P，在平面直角坐标系中，是否存在点Q，使△PAQ是以PA为腰的等腰直角三角形？若存在，写出所有符合条件的点Q的坐标，选择一种情况加以说明；若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是半圆O的直径，半径OC⊥AB于点O，点D是
的中点，连接CD、OD、BD．下列四个结论：①AC∥OD；②CD＝BD；③△ODE∽△CAE；④∠ADC＝∠BOD．其中正确结论的序号是（ ）
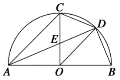
A.①②③④B.①②④C.②③D.①④
查看答案和解析>>
科目：初中数学 来源： 题型：
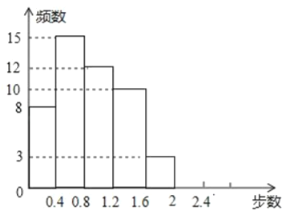
【题目】“微信运动”被越来越多的人关注和喜爱，某兴趣小组随机调查了某市
名教师某日“微信运动”中的步数情况并进行统计整理，绘制了如下的统计图表（不完整） ：请根据以上信息，解答下列问题
写出
的值；
补全频数分布直方图；
若该市约有
名教师，估计日行走步数超过
万步（包含万步）的教师约有多少名？
步数（万步） | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为了解初中学生每天在校体育活动的时间(单位:
)，随机调查了该校的部.分学生，根据调查结果绘制出如下统计图:
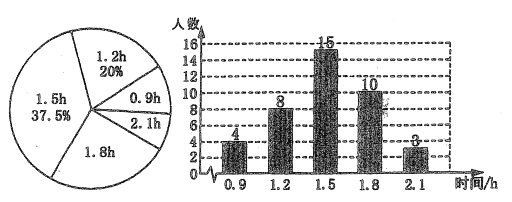
（1）求调查的学生是多少人？ .
（2）求调查的学生每天在校体育活动时间的平均数、众数；
（3）若该校有
名初中学生，估计该校每天在校体育活动时间大于
的学生人数.
查看答案和解析>>
科目：初中数学 来源： 题型：
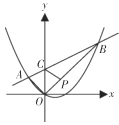
【题目】如图，在平面直角坐标系中，抛物线
上有两点
，
，连接
，
，
，直线交
轴于点
，点到两坐标轴的距离相等．点到两坐标轴的距离也相等．
（1）求点，的坐标并直接写出
的形状；
（2）若点
为线段上的一个动点（不与点
，重合），连接
，当
为等腰三角形时，求点的坐标；
（3）若点
为
轴上一动点，当
是以为斜边的直角三角形时，求点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线
与x轴交于点
，点
，与y轴交于点C，且过点
．点P、Q是抛物线上的动点．
(1)求抛物线的解析式；
(2)当点P在直线OD下方时，求
面积的最大值．
(3)直线OQ与线段BC相交于点E，当
与
相似时，求点Q的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
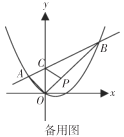
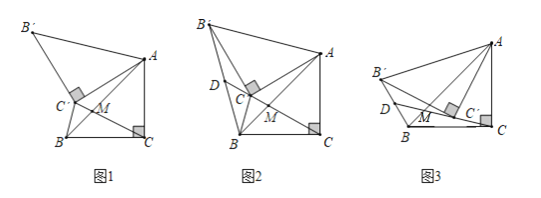
【题目】在△ABC中，∠ACB=90°，BC=AC=2，将△ABC绕点A顺时针方向旋转α角(0°＜α＜180°)至△AB'C'的位置．
问题探究：
（1）如图1，当旋转角为60°时，连接C'C与AB交于点M，则C'C= ，
．
（2）如图2，在（1）条件下，连接BB'，延长CC'交BB'于点D，求CD的长．
问题解决：
（3）如图3，在旋转的过程中，连线CC'、BB'，CC'所在直线交BB'于点D，那么CD的长有没有最大值？如果有，求出CD的最大值：如果没有，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
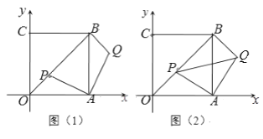
【题目】平面直角坐标系中，四边形OABC是正方形，点A，C 在坐标轴上，点B（
，），P是射线OB上一点，将
绕点A顺时针旋转90°，得
，Q是点P旋转后的对应点.
（1）如图（1）当OP = 
时，求点Q的坐标；
（2）如图（2），设点P（
，
）（
），
的面积为S. 求S与的函数关系式，并写出当S取最小值时，点P的坐标；
（3）当BP+BQ = 
时，求点Q的坐标（直接写出结果即可）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
