
【题目】如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4.
(1)求过A、B、C三点的抛物线的解析式;
(2)设点M是x轴上的动点,试问:在平面直角坐标系中,是否存在点N,使得以点A,B,M,N为顶点的四边形是菱形?若存在,直接写出点N的坐标;若不存在,说明理由;
(3)若抛物线对称轴交x轴于点P,在平面直角坐标系中,是否存在点Q,使△PAQ是以PA为腰的等腰直角三角形?若存在,写出所有符合条件的点Q的坐标,选择一种情况加以说明;若不存在,说明理由.

【答案】(1)y=﹣![]() x2+
x2+![]() x+2(2)(0,﹣2),(
x+2(2)(0,﹣2),(![]() ,2),(﹣
,2),(﹣![]() ,2),(﹣2.5,2)(3)(
,2),(﹣2.5,2)(3)(![]() ,
, ![]() )
)
【解析】试题分析:(1)设抛物线的解析式为y=ax2+bx+c.将点A、B、C的坐标代入得到关于a、b、c的方程,从而可求得a、b、c的值;
(2)分为AB为菱形的边和AB为菱形的对角共可画出4种不同的图形,然后依据菱形对边平行,对角线互相平分的性质确定出点N的坐标即可;
(3)如图5所示:分别以点A和点P为直角的顶点作出等腰直角△APQ,然后由抛物线的对称轴方程求得点P的坐标,过点Q1作Q1M⊥x轴,垂足为M.
然后证明△AOP≌△PMQ1,由全等三角形的性质可求得Q1M=OP=![]() ,PM=OA=2,于是可求得点Q1的坐标.
,PM=OA=2,于是可求得点Q1的坐标.
试题解析:(1)由题意可知;A(0,2)、B(﹣1,0)、C(4,0).
设过A、B、C三点的抛物线的解析式为y=ax2+bx+c.则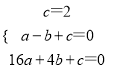 ,解得:
,解得: 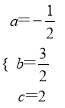
所以抛物线的解析式为y=﹣![]() x2+
x2+![]() x+2.
x+2.
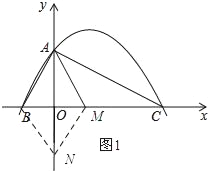
(2)如图1所示:
∵四边形ABNM为菱形,
∴OA=ON.
∴点N的坐标为(0,﹣2).
如图2所示:
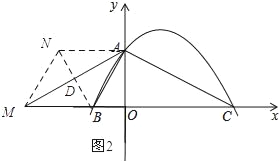
由勾股定理可知:AB=![]() .
.
∵四边形ABMN为菱形,
∴NA∥BM,AN=AB,
∴点N的坐标为(﹣![]() ,2).
,2).
如图3所示;
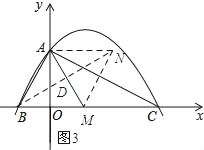
∵四边形ABMN为菱形,
∴NA∥BM,AN=AB.
∴点N的坐标为(![]() ,2).
,2).
如图4所示:
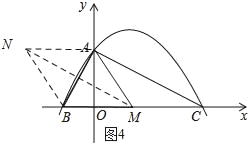
∵四边形ABMN为菱形,
∴NA∥BM,AN=NB.
设点N的坐标为(x,2).由两点间的距离公式可知:(x+1)2+22=x2.
解得:x=﹣2.5.
∴点N的坐标为(﹣2.5,2).
∴点N的坐标为(0,﹣2),(![]() ,2),(﹣
,2),(﹣![]() ,2),(﹣2.5,2).
,2),(﹣2.5,2).
(3)如图5所示:
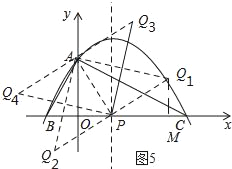
使△PAQ是以PA为腰的等腰直角三角形的所有符合条件的点Q的坐标为Q1(![]() ,
, ![]() ),Q2(﹣
),Q2(﹣![]() ,﹣
,﹣![]() ),Q3(2,
),Q3(2, ![]() ),Q4(﹣2,
),Q4(﹣2, ![]() ).
).
说明Q1:过点Q1作Q1M⊥x轴,垂足为M.
∵x=﹣![]() ,
,
∴P(![]() ,0).
,0).
∴OP=![]() .
.
由题意得;∠APQ1=90°,PA=PQ1.
∴∠OPA+∠CPQ1=90°.
∵∠APO+∠OAP=90°,
∴∠OAP=∠MPQ1.
在△AOP和△PMQ1中,
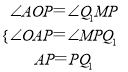 ,
,
∴△AOP≌△PMQ1.
∴Q1M=0P=![]() ,PM=OA=2
,PM=OA=2
∴OM=OP+PM=![]() +2=
+2=![]() .
.
∴点Q1的坐标为(![]() ,
, ![]() ).
).


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知M是△ABC的边AB的中点,D是MC的延长线上一点,满足∠ACM=∠BDM.
(1)求证:AC=BD;
(2)若∠BMC=60°,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD的边AB上的动点,但始终保持EF⊥DE交BC于点F.
(1)求证:△ADE∽△BEF;
(2)若正方形的边长为4,设AE=x,BF=y,求y与x之间的函数解析式;
(3)当x取何值时,y有最大值?并求出这个最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.

(1)求抛物线的函数解析式.
(2)设点D在抛物线上,点E在抛物线的对称轴上,若四边形AODE是平行四边形,求点D的坐标.
(3)联接BC交x轴于点F.y轴上是否存在点P,使得△POC与△BOF相似?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
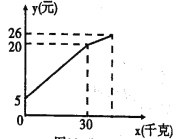
【题目】一农民带了若干千克自产的萝卜进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出萝卜千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)降价前他每千克萝卜出售的价格是多少?
(2)降价后他按每千克0.4元将剩余萝卜售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克萝卜?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形。例如:某三角形三边长分别是5,6和8,因为![]() ,所以这个三角形是常态三角形。
,所以这个三角形是常态三角形。
(1)若△ABC三边长分别是2,![]() 和4,则此三角形_________常态三角形(填“是”或“不是”);
和4,则此三角形_________常态三角形(填“是”或“不是”);
(2)若Rt△ABC是常态三角形,则此三角形的三边长之比为__________________(请按从小到大排列);
(3)如图,Rt△ABC中,∠ACB=90°,BC=6,点D为AB的中点,连接CD,若△BCD是常态三角形,求△ABC的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
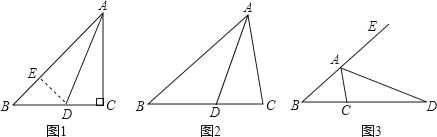
【题目】在△ABC中,∠ACB=2∠B,如图①,当∠C=90°,AD为∠BAC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.
(1)如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?不需要证明,请直接写出你的猜想:
(2)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() ,
,![]() 分别在直线
分别在直线![]() 上,
上,![]() 是平面内一点,
是平面内一点,![]() 和
和![]() 的平分线所在直线相交于点
的平分线所在直线相交于点![]() .
.
(1)如图1,当![]() 都在直线
都在直线![]() 之间,且
之间,且![]() 时,
时,![]() 的度数为_________;
的度数为_________;
(2)如图2,当![]() 都在直线
都在直线![]() 上方时,探究
上方时,探究![]() 和
和![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
(3)如图3,当![]() 在直线
在直线![]() 两侧时,直接写出
两侧时,直接写出![]() 和
和![]() 之间的数量关系是_____.
之间的数量关系是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com