
【题目】如图,AB是半圆O的直径,半径OC⊥AB于点O,点D是![]() 的中点,连接CD、OD、BD.下列四个结论:①AC∥OD;②CD=BD;③△ODE∽△CAE;④∠ADC=∠BOD.其中正确结论的序号是( )
的中点,连接CD、OD、BD.下列四个结论:①AC∥OD;②CD=BD;③△ODE∽△CAE;④∠ADC=∠BOD.其中正确结论的序号是( )
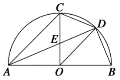
A.①②③④B.①②④C.②③D.①④
【答案】A
【解析】
①如图,利用圆周角定理得∠1=∠3,加上∠1=∠2,则∠2=∠3,于是可得到结论;②利用等弧所对的弦相等即可进行判断;③利用AC∥OD,得到两组角相等,即可得到△ODE∽△CAE;④利用圆周角定理可计算出∠ADC=45°,而∠BOD=45°,则进行判断.
解:①如图,
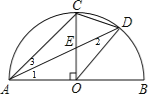
∵点D是![]() 的中点,
的中点,
即![]() ,
,
∴∠1=∠3,
∵OA=OD,
∴∠1=∠2,
∴∠2=∠3,
∴AC∥OD,所以①正确;
②如图连接BD
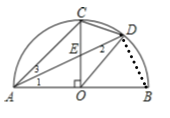
∵点D是![]() 的中点,
的中点,
即![]() ,
,
∴CD=BD,
所以②正确
③∵AC∥OD
∴∠2=∠3,∠EOD=∠ACE
∴△ODE∽△CAE
所以③正确
④∵OC⊥AB
∴∠AOC=∠BOC=90°
∵∠ADC=![]() ∠AOC=45°,∠BOD=
∠AOC=45°,∠BOD=![]() ∠BOC=45°,
∠BOC=45°,
∴∠ADC=∠BOD,所以④正确.
故选:A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,∠CAB的平分线AD交![]() 于点D,过点D作DE∥BC交AC的延长线于点E.
于点D,过点D作DE∥BC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)过点D作DF⊥AB于点F,连接BD.若OF=1,BF=2,求BD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人开车匀速从同一地点到距离出发地480千米处的景点旅游,甲出发半小时后,乙以每小时80千米的速度沿同一路线行驶,两车分别到达目的地后停止.甲、乙两车之间的距离y(千米)与甲车行驶的时间x(小时)之间的函数关系如图所示.
(1)甲行驶的速度是 千米/小时.
(2)求乙车追上甲车后,y与x之间的函数关系式,并写出自变量x的取值范围.
(3)求甲车出发多长时间两车相距75千米.
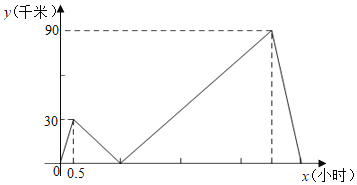
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式规律:① 52-22=3×7;②72-42=3×11;③ 92-62=3×11;…;根据上面等式的规律:
(1)写出第6个和第n个等式;
(2)证明你写的第n个等式的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代人对于健康越来越重视,比起去健身房或者运动量较大的户外活动,不少人更钟爱健步走.如今,在朋友圈里晒步数拼排行抢封面是不少人健步走的乐趣所在,“日行万步”已经成为众多运动爱好者的标配,在一次社会调查活动中,小李随机抽取某“健步走运动”团队20名成员,收集他们一天行走的步数,记录如下:
5640 | 6430 | 6520 | 6798 | 7325 |
8430 | 8215 | 7453 | 7446 | 6754 |
7638 | 6834 | 7326 | 6830 | 8648 |
8752 | 9450 | 9865 | 7290 | 7850 |
对这20个数据按组距1000进行分组,并统计整理,绘制了如下不完整的统计图表.
组别 | 步数分组 |
A |
|
B |
|
C |
|
D |
|
E |
|
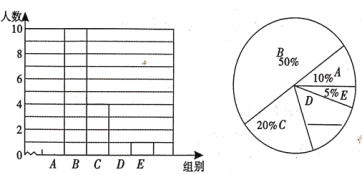
根据以上信息解答下列问题:
(1)补全两幅统计图;
(2)这20名“健步走运动”团队成员一天行走的步数的中位数落在 组;其中D组.数据的平均数 步;
(3)若该团队共有200人,请估计其中一天行走步数少于8500步的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
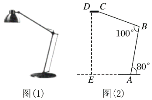
【题目】如图(1)是小明家购买的一款台灯,现忽略支架的粗细,得到它的侧面简化示意图如图(2)所示.支架AB与桌面的夹角为80°,支架AB与支架BC的夹角为100°,CD平行于桌面,支架AB,BC的长度均为20cm.求灯泡顶端D到桌面的距离DE.(结果精确到1cm.参考数据:sin80°≈0.98,cos80°≈0.17,tan80°≈5.67,sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
查看答案和解析>>
科目:初中数学 来源: 题型:
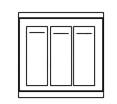
【题目】小明家客厅里装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,按下任意一个开关均可打开对应的一盏电灯,因刚搬进新房不久,不熟悉情况.
(1)若小明任意按下一个开关,则小明打开走廊灯的概率是多少?
(2)若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图法或列表法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,②,在平面直角坐标系xoy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,![]() , P是x轴上的一动点,连结CP。
, P是x轴上的一动点,连结CP。
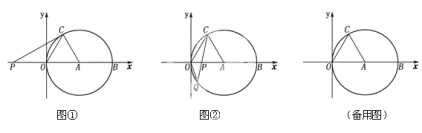
(1)求![]() 的度数;
的度数;
(2)如图①,当CP与⊙A相切时,求PO的长;
(3)如图②,当点P在直径OB上时,CP的延长线与⊙A相交于点Q,问PO为何值时,![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com