
【题目】如图,在![]() 上依次有
上依次有![]() 三点,
三点,![]() 的延长线交
的延长线交![]() 于
于![]() ,
,![]() 过点
过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() 交
交![]() 于点
于点![]() .连接
.连接![]() , 若
, 若![]() 且
且![]() ,则劣弧
,则劣弧![]() 的长是( )
的长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
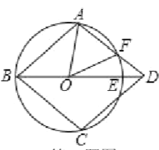
先证明四边形ABCD是菱形,得到AD∥BC;设∠FOE=x,则∠AOF=3x,根据∠ABC+∠BAD=180°,列方程得:4x+2x+![]() (180-3x)=180,求出x的值;然后求CF所对的圆心角和半径的长,最后根据弧长公式即可解答.
(180-3x)=180,求出x的值;然后求CF所对的圆心角和半径的长,最后根据弧长公式即可解答.
解:∵![]()
∴∠CBD=∠ABD
∵CD//AB.
∴∠ABD=∠CDB,
∴∠CBD=∠CDB
∴CB=CD.
∴BE是圆O的直径
∴![]()
∴AB=BC=CD
∵CD//AB
∴.四边形ABCD是菱形
∴AD∥BC
设∠FOE=x,则∠AOF=3x,∠AOD=∠FOE+∠AOF=4x
∵OA=OF.
∴∠OAF=∠OFA=![]() (180-3x)°
(180-3x)°
∵OA=OB,
∴∠OAB=∠OBA=2x,
∴∠ABC=4x,
∵BC∥AD.
∴∠ABC+ ∠BAD=180°
∴4x+2x+![]() (180-3x)=180,解得x=20°
(180-3x)=180,解得x=20°
∴∠AOF=3x=60°,∠AOE=80°
∴∠COF=80°×2-60°=100°
∵OA=OF
∴△AOF是等边三角形
∵OF=AF=2
∴![]() 的长=
的长=![]()
故答案为C.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .垂直于
.垂直于![]() 轴的直线
轴的直线![]() 与抛物线交于点
与抛物线交于点![]() ,
,![]() ,与直线
,与直线![]() 交于点
交于点![]() ,若
,若![]() ,记
,记![]() ,则
,则![]() 的取值范围为( )
的取值范围为( )
A.5<s<6B.6<s<7C.7<s<8D.8<s<9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC是直角三角形,∠ABC=90°,∠CAB=60°,点O(0,0),点A(1,0),点B(﹣1,0),点C在第二象限,点P(﹣2,![]() ).
).
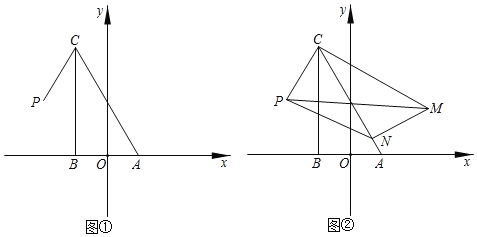
(I)如图①,求C点坐标及∠PCB的大小;
(II)将△ABC绕C点逆时针旋转得到△MNC,点A,B的对应点分别为点M,N,S为△PMN的面积.
①如图②,当点N落在边CA上时,求S的值;
②求S的取值范围(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
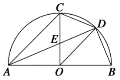
【题目】如图,AB是半圆O的直径,半径OC⊥AB于点O,点D是![]() 的中点,连接CD、OD、BD.下列四个结论:①AC∥OD;②CD=BD;③△ODE∽△CAE;④∠ADC=∠BOD.其中正确结论的序号是( )
的中点,连接CD、OD、BD.下列四个结论:①AC∥OD;②CD=BD;③△ODE∽△CAE;④∠ADC=∠BOD.其中正确结论的序号是( )
A.①②③④B.①②④C.②③D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组对函数![]() 的图象和性质进行了研究,探究过程如下.
的图象和性质进行了研究,探究过程如下.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下.
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 8 | m | 0 | 2 | n | 2 | 0 |
| 8 | … |
其中,m= ,n= ;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请补全函数图象的剩余部分;
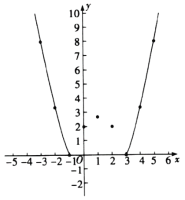
(3)进一步探究函数图象发现:
①函数图象与x轴有_____________个交点;
②方程![]() 有_____________个实数根;
有_____________个实数根;
③当关于x的方程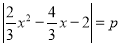 有3个实数根时,p的值是_____________.
有3个实数根时,p的值是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
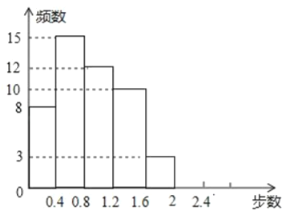
【题目】“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了某市![]() 名教师某日“微信运动”中的步数情况并进行统计整理,绘制了如下的统计图表(不完整) :请根据以上信息,解答下列问题
名教师某日“微信运动”中的步数情况并进行统计整理,绘制了如下的统计图表(不完整) :请根据以上信息,解答下列问题
![]() 写出
写出![]() 的值;
的值;
![]() 补全频数分布直方图;
补全频数分布直方图;
![]() 若该市约有
若该市约有![]() 名教师,估计日行走步数超过
名教师,估计日行走步数超过![]() 万步(包含
万步(包含![]() 万步)的教师约有多少名?
万步)的教师约有多少名?
步数(万步) | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解初中学生每天在校体育活动的时间(单位:![]() ),随机调查了该校的部.分学生,根据调查结果绘制出如下统计图:
),随机调查了该校的部.分学生,根据调查结果绘制出如下统计图:
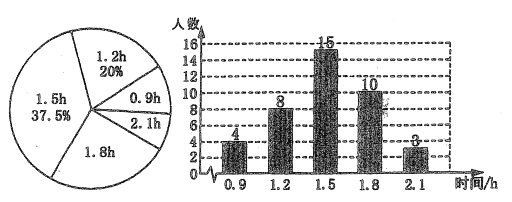
(1)求调查的学生是多少人? .
(2)求调查的学生每天在校体育活动时间的平均数、众数;
(3)若该校有![]() 名初中学生,估计该校每天在校体育活动时间大于
名初中学生,估计该校每天在校体育活动时间大于![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,点
,点![]() ,与y轴交于点C,且过点
,与y轴交于点C,且过点![]() .点P、Q是抛物线
.点P、Q是抛物线![]() 上的动点.
上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求![]() 面积的最大值.
面积的最大值.
(3)直线OQ与线段BC相交于点E,当![]() 与
与![]() 相似时,求点Q的坐标.
相似时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
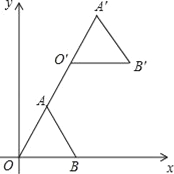
【题目】如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
A. (4,2![]() ) B. (3,3
) B. (3,3![]() ) C. (4,3
) C. (4,3![]() ) D. (3,2
) D. (3,2![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com