
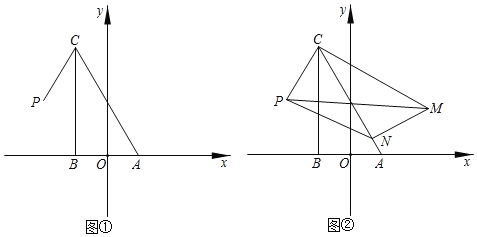
【题目】在平面直角坐标系中,△ABC是直角三角形,∠ABC=90°,∠CAB=60°,点O(0,0),点A(1,0),点B(﹣1,0),点C在第二象限,点P(﹣2,![]() ).
).
(I)如图①,求C点坐标及∠PCB的大小;
(II)将△ABC绕C点逆时针旋转得到△MNC,点A,B的对应点分别为点M,N,S为△PMN的面积.
①如图②,当点N落在边CA上时,求S的值;
②求S的取值范围(直接写出结果即可).
【答案】(Ⅰ)C(﹣1,2![]() ),∠PCB=30°;(Ⅱ)①2
),∠PCB=30°;(Ⅱ)①2![]() 1;②S的取值范围为2
1;②S的取值范围为2![]() 2.
2.
【解析】
(Ⅰ)根据点A(1,0),点B(﹣1,0)得到AB=2,利用锐角三角函数求出BC=ABtan60°=2![]() 2
2![]() ,得到C(﹣1,2
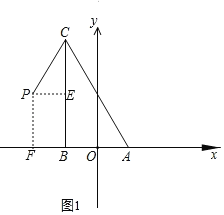
,得到C(﹣1,2![]() ).过点P作PE⊥CB,垂足为点E,过点P作PF⊥x轴,垂足为点F,证明四边形PFBE为矩形,利用P(﹣2,
).过点P作PE⊥CB,垂足为点E,过点P作PF⊥x轴,垂足为点F,证明四边形PFBE为矩形,利用P(﹣2,![]() )求出PE=FB=1,CE=CB﹣BE=2
)求出PE=FB=1,CE=CB﹣BE=2![]() ,由tan∠PCE
,由tan∠PCE![]() 得到∠PCB=30°;
得到∠PCB=30°;
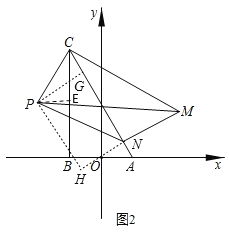
(Ⅱ)①如图2,过点P作PH⊥直线MN,垂足为点H,过点P作PG⊥AC,垂足为点G,则四边形PHNG为矩形得到PH=GN,由旋转的性质得到CN=CB=2![]() ,MN=AB=2,由(Ⅰ)可知∠PCB=30°,PE=1,求出PC=2,∠PCG=∠PCB+∠BCA=60°,得到PH=GN=CN﹣CG=CB﹣CG=2
,MN=AB=2,由(Ⅰ)可知∠PCB=30°,PE=1,求出PC=2,∠PCG=∠PCB+∠BCA=60°,得到PH=GN=CN﹣CG=CB﹣CG=2![]() 1,由三角形的面积公式求出S
1,由三角形的面积公式求出S![]() MNPH
MNPH![]() 2×PH=PH=2
2×PH=PH=2![]() 1;
1;
②分两种情况:如图3,当点N在PC的延长线上时,S△PMN最大,如图4,当点N在CP的延长线上时,S△PMN最小,由此得到答案.
(Ⅰ)∵点A(1,0),点B(﹣1,0),
∴OA=1,OB=1,
∴AB=2,
在Rt△ABC中,∠CAB=60°.
∵tan∠CAB![]() ,
,
∴BC=ABtan60°=2![]() 2
2![]() ,
,
∴C(﹣1,2![]() ).
).
如图1,过点P作PE⊥CB,垂足为点E,过点P作PF⊥x轴,垂足为点F,
∴∠PFB=∠PEB=90°.
∵∠ABC=∠FBC=90°,
∴四边形PFBE为矩形.
∵P(﹣2,![]() ),
),
∴OF=2,PF![]() ,
,
∴FB=OF﹣OB=1,
∴BE=PF![]() ,PE=FB=1,
,PE=FB=1,
∴CE=CB﹣BE=2![]() .
.
在Rt△CPE中,
∵tan∠PCE![]() ,
,
∴∠PCB=30°.
(Ⅱ)①如图2,过点P作PH⊥直线MN,垂足为点H,过点P作PG⊥AC,垂足为点G,则四边形PHNG为矩形,
∴PH=GN.
∵△MNC是由△ABC旋转得到的,
∴CN=CB=2![]() ,MN=AB=2.
,MN=AB=2.
∵∠ABC=90°,∠CAB=60°,
∴∠BCA=30°,
由(Ⅰ)可知∠PCB=30°,PE=1,
∴PC=2,∠PCG=∠PCB+∠BCA=60°.
在Rt△PCG中,∠CPG=30°,
∴CG![]() PC=1,
PC=1,
∴PH=GN=CN﹣CG=CB﹣CG=2![]() 1,
1,
∴S![]() MNPH
MNPH![]() 2×PH=PH=2
2×PH=PH=2![]() 1.
1.
②S的取值范围为2![]() 2.
2.
如图3,当点N在PC的延长线上时,S△PMN最大.
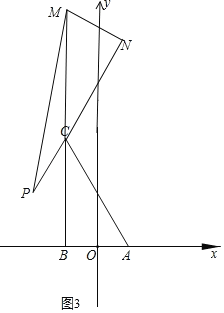
此时PN=PC+CN=2+2![]() ,
,
∴S![]() 2
2![]() 2.
2.
如图4,当点N在CP的延长线上时,S△PMN最小.
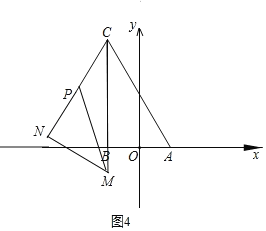
此时PN=CN﹣CP=2![]() 2,
2,
∴S![]() 2
2![]() 2
2![]() 2,
2,
∴2![]() 2.
2.
即S的取值范围为2![]() 2.
2.


科目:初中数学 来源: 题型:
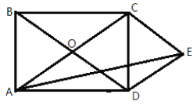
【题目】如图,矩形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,AB与BC的比是黄金比,过点C作CE∥BD,过点D作DE∥AC,DE、
,AB与BC的比是黄金比,过点C作CE∥BD,过点D作DE∥AC,DE、![]() 交于点
交于点![]() ,连接AE,则tan∠DAE的值为___________.(不取近似值)
,连接AE,则tan∠DAE的值为___________.(不取近似值)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求菱形BMDN的周长和对角线MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
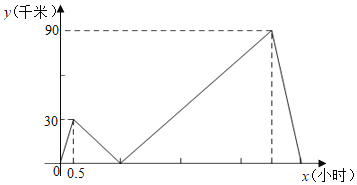
【题目】甲、乙两人开车匀速从同一地点到距离出发地480千米处的景点旅游,甲出发半小时后,乙以每小时80千米的速度沿同一路线行驶,两车分别到达目的地后停止.甲、乙两车之间的距离y(千米)与甲车行驶的时间x(小时)之间的函数关系如图所示.
(1)甲行驶的速度是 千米/小时.
(2)求乙车追上甲车后,y与x之间的函数关系式,并写出自变量x的取值范围.
(3)求甲车出发多长时间两车相距75千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
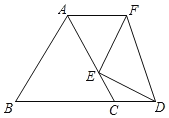
【题目】如图,△ABC是等边三角形,AB=3,点E在AC上,AE![]() AC,D是BC延长线上一点,将线段DE绕点E逆时针旋转90°得到线段FE,当AF∥BD时,线段AF的长为____.
AC,D是BC延长线上一点,将线段DE绕点E逆时针旋转90°得到线段FE,当AF∥BD时,线段AF的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式规律:① 52-22=3×7;②72-42=3×11;③ 92-62=3×11;…;根据上面等式的规律:
(1)写出第6个和第n个等式;
(2)证明你写的第n个等式的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代人对于健康越来越重视,比起去健身房或者运动量较大的户外活动,不少人更钟爱健步走.如今,在朋友圈里晒步数拼排行抢封面是不少人健步走的乐趣所在,“日行万步”已经成为众多运动爱好者的标配,在一次社会调查活动中,小李随机抽取某“健步走运动”团队20名成员,收集他们一天行走的步数,记录如下:
5640 | 6430 | 6520 | 6798 | 7325 |
8430 | 8215 | 7453 | 7446 | 6754 |
7638 | 6834 | 7326 | 6830 | 8648 |
8752 | 9450 | 9865 | 7290 | 7850 |
对这20个数据按组距1000进行分组,并统计整理,绘制了如下不完整的统计图表.
组别 | 步数分组 |
A |
|
B |
|
C |
|
D |
|
E |
|
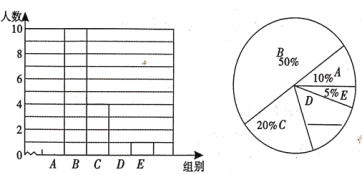
根据以上信息解答下列问题:
(1)补全两幅统计图;
(2)这20名“健步走运动”团队成员一天行走的步数的中位数落在 组;其中D组.数据的平均数 步;
(3)若该团队共有200人,请估计其中一天行走步数少于8500步的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
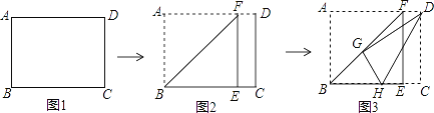
【题目】如图1,有一张矩形纸片ABCD,已知AB=10,AD=12,现将纸片进行如下操作:现将纸片沿折痕BF进行折叠,使点A落在BC边上的点E处,点F在AD上(如图2);然后将纸片沿折痕DH进行第二次折叠,使点C落在第一次的折痕BF上的点G处,点H在BC上(如图3),给出四个结论:
①AF的长为10;②△BGH的周长为18;③![]() =
=![]() ;④GH的长为5,
;④GH的长为5,
其中正确的结论有________.(写出所有正确结论的番号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com