
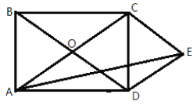
【题目】如图,矩形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,AB与BC的比是黄金比,过点C作CE∥BD,过点D作DE∥AC,DE、
,AB与BC的比是黄金比,过点C作CE∥BD,过点D作DE∥AC,DE、![]() 交于点
交于点![]() ,连接AE,则tan∠DAE的值为___________.(不取近似值)
,连接AE,则tan∠DAE的值为___________.(不取近似值)
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.这本书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.用现代白话文可以这样理解:甲口袋中装有黄金9枚(每枚黄金重量相同),乙口袋中装有白银11枚(每枚白银重量相同),用称分别称这两个口袋的重量,它们的重量相等.若从甲口袋中拿出1枚黄金放入乙口袋中,乙口袋中拿出1枚白银放入甲口袋中,则甲口袋的重量比乙口袋的重量轻了13两(袋子重量忽略不计).问一枚黄金和一枚白银分别重多少两?请根据题意列方程(组)解之.
查看答案和解析>>
科目:初中数学 来源: 题型:
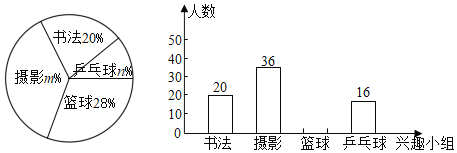
【题目】某校计划组织学生参加学校书法、摄影、篮球、乒乓球四个课外兴趣小组,要求每人必须参加并且只能选择其中的一个小组,为了了解学生对四个课外小组的选择情况,学校从全体学生中随机抽取部分学生进行问卷调查,并把调查结果制成如图所示的两幅不完整的统计图,请你根据给出的信息解答下列问题:
(1)求该校参加这次问卷调查的学生人数,并补全条形统计图(画图后请标注相应的数据);
(2)m= ,n= ;
(3)若该校共有2000名学生,试估计该校选择“乒乓球”课外兴趣小组的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
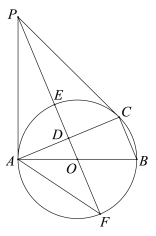
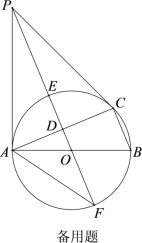
【题目】如图,⊙O是△ABC的外接圆,AB是直径,D是AC中点,直线OD与⊙O相交于E,F两点,P是⊙O外一点,P在直线OD上,连接PA,PC,AF,且满足∠PCA=∠ABC.
(1)求证:PA是⊙O的切线;
(2)证明:![]() ;
;
(3)若BC=8,tan∠AFP=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
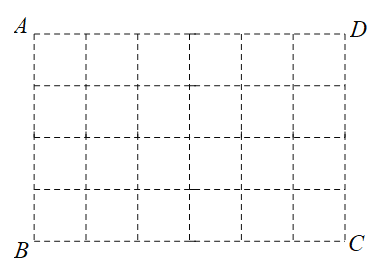
【题目】如图,在6×4的方格纸ABCD中,请按要求画格点线段(端点在格点上),且线段的端点均不与点A,B,C,D重合.
(1)在图1中画格点线段EF,GH各一条,使点E,F,G,H分别落在边AB,BC,CD,DA上,且EF=GH,EF不平行GH;
(2)在图2中画格点线段MN,PQ各一条,使点M,N,P,Q分别落在边AB,BC,CD,DA上,且PQ=![]() MN.
MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小寇随机调查了若干租用共享单车市民的骑车时间t(单位:分),将获得的据分成四组(A:0<t≤10,B:10<t≤20,C:20<t≤30, D:t>30),绘制了如下统计图,根据图中信息,解答下列问题:
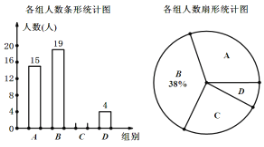
(1)小寇调查的总人数是 人;
(2)表示C组的扇形统计图的圆心角的度数是 °;
(3)如果小寇想从D组的甲、乙、丙、丁四人中随机选择两人进一步了解平时租用共享单车情况,请用列表或画树状图的方法求出丁被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
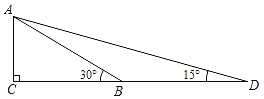
【题目】构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°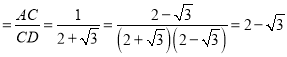 .类比这种方法,计算tan22.5°的值为( )
.类比这种方法,计算tan22.5°的值为( )
A.![]() B.
B.![]() ﹣1C.
﹣1C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .垂直于
.垂直于![]() 轴的直线
轴的直线![]() 与抛物线交于点
与抛物线交于点![]() ,
,![]() ,与直线
,与直线![]() 交于点
交于点![]() ,若
,若![]() ,记
,记![]() ,则
,则![]() 的取值范围为( )
的取值范围为( )
A.5<s<6B.6<s<7C.7<s<8D.8<s<9
查看答案和解析>>
科目:初中数学 来源: 题型:
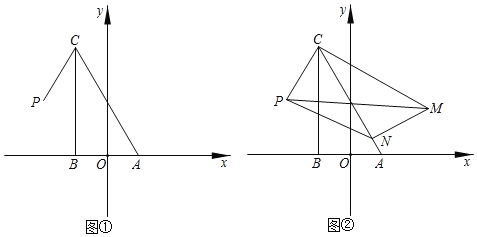
【题目】在平面直角坐标系中,△ABC是直角三角形,∠ABC=90°,∠CAB=60°,点O(0,0),点A(1,0),点B(﹣1,0),点C在第二象限,点P(﹣2,![]() ).
).
(I)如图①,求C点坐标及∠PCB的大小;
(II)将△ABC绕C点逆时针旋转得到△MNC,点A,B的对应点分别为点M,N,S为△PMN的面积.
①如图②,当点N落在边CA上时,求S的值;
②求S的取值范围(直接写出结果即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com