
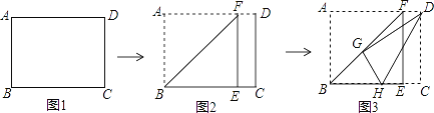
【题目】如图1,有一张矩形纸片ABCD,已知AB=10,AD=12,现将纸片进行如下操作:现将纸片沿折痕BF进行折叠,使点A落在BC边上的点E处,点F在AD上(如图2);然后将纸片沿折痕DH进行第二次折叠,使点C落在第一次的折痕BF上的点G处,点H在BC上(如图3),给出四个结论:
①AF的长为10;②△BGH的周长为18;③![]() =
=![]() ;④GH的长为5,
;④GH的长为5,
其中正确的结论有________.(写出所有正确结论的番号)
【答案】①③④
【解析】
过G点作MN∥AB,交AD、BC于点M、N,可知四边形ABEF为正方形,可求得AF的长,可判断①,且△BNG和△FMG为等腰三角形,设BN=x,则可表示出GN、MG、MD,利用折叠的性质可得到CD=DG.在Rt△MDG中,利用勾股定理可求得x,再利用△MGD∽△NHG,可求得NH、GH和HC,则可求得BH,容易判断②③④,可得出答案.
如图,过点G作MN∥AB,分别交AD、BC于点M、N.
∵四边形ABCD为矩形,∴AB=CD=10,BC=AD=12,由折叠可得:AB=BE,且∠A=∠ABE=∠BEF=90°,∴四边形ABEF为正方形,∴AF=AB=10,故①正确;
∵MN∥AB,∴△BNG和△FMG为等腰直角三角形,且MN=AB=10,设BN=x,则GN=AM=x,MG=MN﹣GN=10﹣x,MD=AD﹣AM=12﹣x,又由折叠的可知DG=DC=10.在Rt△MDG中,由勾股定理可得:MD2+MG2=GD2,即(12﹣x)2+(10﹣x)2=102,解得:x=18(舍去),x=4,∴GN=BN=4,MG=6,MD=8,又∠DGH=∠C=∠GMD=90°,∴∠NGH+∠MGD=∠MGD+∠MDG=90°,∴∠NGH=∠MDG,且∠DMG=∠GNH,∴△MGD∽△NHG,∴![]() ,即
,即![]() ,∴NH=3,GH=CH=5,∴BH=BC﹣HC=12﹣5=7,故④正确;
,∴NH=3,GH=CH=5,∴BH=BC﹣HC=12﹣5=7,故④正确;
又∵△BNG和△FMG为等腰直角三角形,且BN=4,MG=6,∴BG=4![]() ,GF=6
,GF=6![]() ,∴△BGH的周长=BG+GH+BH=4
,∴△BGH的周长=BG+GH+BH=4![]() 5+7=12+4
5+7=12+4![]() ,故②不正确;③正确;
,故②不正确;③正确;
综上可知正确的为①③④.
故答案为①③④.


科目:初中数学 来源: 题型:
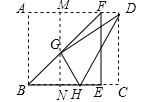
【题目】在平面直角坐标系中,△ABC是直角三角形,∠ABC=90°,∠CAB=60°,点O(0,0),点A(1,0),点B(﹣1,0),点C在第二象限,点P(﹣2,![]() ).
).
(I)如图①,求C点坐标及∠PCB的大小;
(II)将△ABC绕C点逆时针旋转得到△MNC,点A,B的对应点分别为点M,N,S为△PMN的面积.
①如图②,当点N落在边CA上时,求S的值;
②求S的取值范围(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解初中学生每天在校体育活动的时间(单位:![]() ),随机调查了该校的部.分学生,根据调查结果绘制出如下统计图:
),随机调查了该校的部.分学生,根据调查结果绘制出如下统计图:
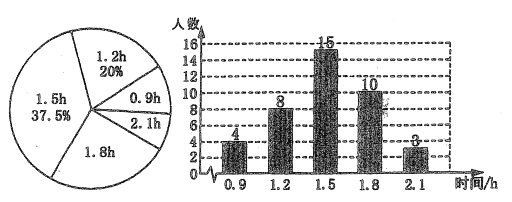
(1)求调查的学生是多少人? .
(2)求调查的学生每天在校体育活动时间的平均数、众数;
(3)若该校有![]() 名初中学生,估计该校每天在校体育活动时间大于
名初中学生,估计该校每天在校体育活动时间大于![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,点
,点![]() ,与y轴交于点C,且过点
,与y轴交于点C,且过点![]() .点P、Q是抛物线
.点P、Q是抛物线![]() 上的动点.
上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求![]() 面积的最大值.
面积的最大值.
(3)直线OQ与线段BC相交于点E,当![]() 与
与![]() 相似时,求点Q的坐标.
相似时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
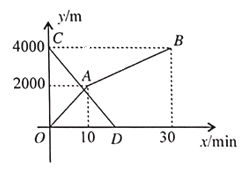
【题目】小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步中途改为步行,到达图书馆恰好用![]() .小东骑自行车以
.小东骑自行车以![]() 的速度直接回家,两人离家的路程
的速度直接回家,两人离家的路程![]() 与各自离开出发 地的时间之间
与各自离开出发 地的时间之间![]() 的函数图象如图所示.
的函数图象如图所示.
![]() 家与图书馆之间的路程为多少
家与图书馆之间的路程为多少![]() ,小玲步行的速度为多少
,小玲步行的速度为多少![]() ;
;
![]() 求小东离家的路程
求小东离家的路程![]() 关于
关于![]() 的函数解析式,并写出自变量的取值范围;
的函数解析式,并写出自变量的取值范围;
![]() 求两人相遇时离家多远?
求两人相遇时离家多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
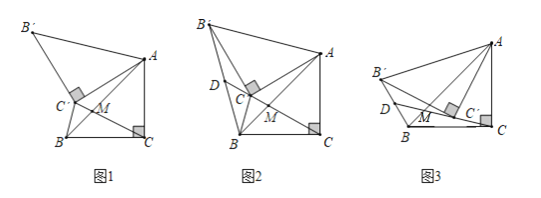
【题目】在△ABC中,∠ACB=90°,BC=AC=2,将△ABC绕点A顺时针方向旋转α角(0°<α<180°)至△AB'C'的位置.
问题探究:
(1)如图1,当旋转角为60°时,连接C'C与AB交于点M,则C'C= ,![]() .
.
(2)如图2,在(1)条件下,连接BB',延长CC'交BB'于点D,求CD的长.
问题解决:
(3)如图3,在旋转的过程中,连线CC'、BB',CC'所在直线交BB'于点D,那么CD的长有没有最大值?如果有,求出CD的最大值:如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
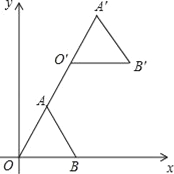
【题目】如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
A. (4,2![]() ) B. (3,3
) B. (3,3![]() ) C. (4,3
) C. (4,3![]() ) D. (3,2
) D. (3,2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
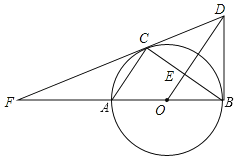
【题目】如图,已知AB是⊙O的直径,AC,BC是⊙O的弦,OE∥AC交BC于E,过点B作⊙O的切线交OE的延长线于点D,连接DC并延长交BA的延长线于点F.
(1)求证:DC是⊙O的切线;
(2)若∠ABC=30°,AB=8,求线段CF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com