
【题目】解不等式组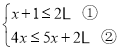 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(1)解不等式①,得_________________;
(2)解不等式②,得_________________;
(3)把不等式①和②的解集在数轴上表示出来:
![]()
(4)原不等式组的解集为_________________.
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】某校为了解初中学生每天在校体育活动的时间(单位:![]() ),随机调查了该校的部.分学生,根据调查结果绘制出如下统计图:
),随机调查了该校的部.分学生,根据调查结果绘制出如下统计图:
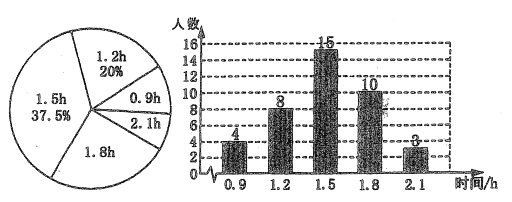
(1)求调查的学生是多少人? .
(2)求调查的学生每天在校体育活动时间的平均数、众数;
(3)若该校有![]() 名初中学生,估计该校每天在校体育活动时间大于
名初中学生,估计该校每天在校体育活动时间大于![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
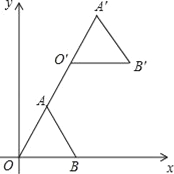
【题目】如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内,将△OAB沿直线OA的方向平移至△O′A′B′的位置,此时点A′的横坐标为3,则点B′的坐标为( )
A. (4,2![]() ) B. (3,3
) B. (3,3![]() ) C. (4,3
) C. (4,3![]() ) D. (3,2
) D. (3,2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
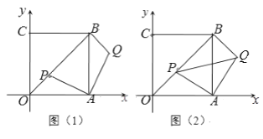
【题目】平面直角坐标系中,四边形OABC是正方形,点A,C 在坐标轴上,点B(![]() ,
,![]() ),P是射线OB上一点,将
),P是射线OB上一点,将![]() 绕点A顺时针旋转90°,得
绕点A顺时针旋转90°,得![]() ,Q是点P旋转后的对应点.
,Q是点P旋转后的对应点.
(1)如图(1)当OP = ![]() 时,求点Q的坐标;
时,求点Q的坐标;
(2)如图(2),设点P(![]() ,
,![]() )(
)(![]() ),
),![]() 的面积为S. 求S与
的面积为S. 求S与![]() 的函数关系式,并写出当S取最小值时,点P的坐标;
的函数关系式,并写出当S取最小值时,点P的坐标;
(3)当BP+BQ = ![]() 时,求点Q的坐标(直接写出结果即可)
时,求点Q的坐标(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某旅游景区为方便游客,修建了一条东西走向的栈道AB,栈道AB与景区道路CD平行.在C处测得栈道一端A位于北偏西45°方向,在D处测得栈道另一端B位于北偏东32°方向.已知AC=60 m ,CD=46 m,求栈道AB的长(结果保留整数).参考数据:sin32° ≈ 0.53,cos32° ≈ 0.85,tan32° ≈ 0.62,![]() ≈ 1.414.
≈ 1.414.

查看答案和解析>>
科目:初中数学 来源: 题型:
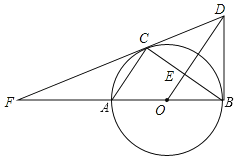
【题目】如图,已知AB是⊙O的直径,AC,BC是⊙O的弦,OE∥AC交BC于E,过点B作⊙O的切线交OE的延长线于点D,连接DC并延长交BA的延长线于点F.
(1)求证:DC是⊙O的切线;
(2)若∠ABC=30°,AB=8,求线段CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
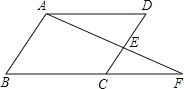
【题目】如图,点E是ABCD的边CD的中点,连结AE并延长,交BC的延长线于点F.
(1)若AD的长为2.求CF的长.
(2)若∠BAF=90°,试添加一个条件,并写出∠F的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com