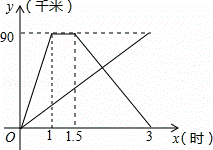
甲、乙两人同时从相距90千米的A地前往B地，甲乘汽车，乙骑摩托车，甲到达B地停留半小时后返回A地．如图是他们离A地的距离y（千米）与时间x（时）之间的函数关系图象．
（1
）求甲从B地返回A地的过程中，y与x之间的函数关系式，并写出自变量x的取值范围；
（2）若乙出发后2小时和甲相遇，求乙从A地到B地用了多长时间？
科目：初中数学 来源： 题型：
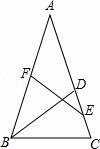
如图，在△ABC中，D是边AC上一点，且BD=BC，点E、F分别是DC、AB的中点．求证：
（1）EF=
AB；
（2）过A点作AG∥EF，交BE的延长线于点G，则BE=GE．
查看答案和解析>>
科目：初中数学 来源： 题型：
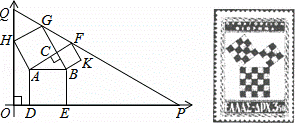
勾股定理有着悠久的历史，它曾引起很多人的兴趣，1955年希腊发型了二枚以勾股图为背景的邮票．所谓勾股图是指以直角三角形的三边为边向外作正方形构成，它可以验证勾股定理．在如图的勾股图中，已知∠ACB=90°，∠BAC=30°，AB=4．作△PQO使得∠O=90°，点Q在在直角坐标系y轴正半轴上，点P在x轴正半轴上，点O与原点重合，∠OQP=60°，点H在边QO上，点D、E在边PO上，点G、F在边PQ上，那么点P坐标为 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
，
已知一次函数y=2x+b交x轴于点A（﹣2，0），交y轴于点B，则点B坐标为 
B． 直线
C． y轴 D． 直线x=2