
分析 (1)把A和B的坐标代入抛物线解析式,得到关于a与b的二元一次方程组,求出方程组的解集得到a与b的值,进而确定出抛物线的解析式;
(2)在第二象限图象的抛物线上任取一点E,过E作EF垂直于x轴,垂足为F,连接BE,EC,BC,△BEC的面积=△BEF的面积+梯形COFE的面积-△BOC的面积,由抛物线与y轴的交点为C,求出C的坐标得到OC的长,由B的坐标得到OB的长,又△BOC为直角三角形,两直角边OB与OC乘积的一半即为△BOC的面积,此面积为定值,故要求△BEC面积的最大值,即要求三角形BEF的面积+梯形COFE的面积的最大值,设出E的坐标(m,-m2-2m+3),EF为E的纵坐标,OF为E横坐标的绝对值,BF=OB-OF,而△BEF为直角三角形,利用两直角边EF与BF乘积的一半表示出此三角形的面积,再根据上下底之和的一半乘以高表示出梯形OCFE的面积,进而表示出△BEF的面积+梯形COFE的面积之和,配方后根据二次项系数小于0,得到抛物线开口向下,二次函数有最大值,利用二次函数的性质求出此时面积之和的最大值,用求出面积之和的最大值减去△BOC的面积,即可得到△BEC面积的最大值,由此时求出的m,可确定出此时E的坐标;
(3)由点A和点B关于x轴对称,连接BC交对称轴与点P,则点P就是使△PAC的周长最小的点,由于抛物线y=-x2-2x+3的对称轴为x=-1,点P在抛物线的对称轴上,于是设P(-1,b),求得直线BC的解析式为y=-x+3,把P(-1,b)代入y=-x+3即可得到结论;
(4)存在,设P(-1,b),Q(a,-a2-2a+3),根据勾股定理得到AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,根据平行四边形的性质得到PQ=AC,PQ∥AC,过Q作QH⊥对称轴于H,推出△ACO∽△PQH,根据相似三角形的性质得到$\frac{OA}{OC}$=$\frac{QH}{PH}$,求得b=-a2+a+6,根据两点间的距离公式得到$\sqrt{(-1-a)^{2}+(b+{a}^{2}+2a-3)^{2}}$=$\sqrt{10}$,于是得到方程(1+a)2+(-a2+a+6+a2+2a-3)2=10,解得a=-2,于是得到结论.
解答 解:(1)∵y=a(x2+2x-3)(a≠0)与x轴交于点A和点B,
∴当y=0时,即a(x2+2x-3)=0,解得:x1=-3,x2=1,
∴A(1,0),B(-3,0),
∵OC=OB,
∴OC=OB=3,
∴C(0,3),
把C(0,3)代入y=a(x2+2x-3)得:3=a(-3),
解得a=-1,
∴抛物线的解析式为:y=-x2-2x+3;
(2)如图1,过点E作EF⊥x轴于点F,连接BE,FC,BC,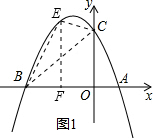 设E(m,-m2-2m+3)(-3<m<0),
设E(m,-m2-2m+3)(-3<m<0),
∴EF=-m2-2m+3,BF=m+3,OF=-m,
∴S四边形BOCE=$\frac{1}{2}$BF•EF+$\frac{1}{2}$(OC+EF)•OF
=$\frac{1}{2}$(m+3)•(-m2-2m+3)+$\frac{1}{2}$(-m2-2m+6)•(-m)
=-$\frac{3}{2}$m2-$\frac{9}{2}$m+$\frac{9}{2}$=-$\frac{3}{2}$(m+$\frac{3}{2}$)2+$\frac{63}{8}$,
∴当m=-$\frac{3}{2}$时,S四边形BOCE最大,且最大值为$\frac{63}{8}$,
而S△BOC值一定,具体求法如下:
∵B(-3,0),C(0,3),
∴OB=3,OC=3,
∴S△BOC=$\frac{1}{2}$OB•OC=$\frac{9}{2}$,
则△BCE面积的最大值S=S四边形BOCE-S△BOC=$\frac{63}{8}$-$\frac{9}{2}$=$\frac{27}{8}$,
又∵当m=-$\frac{3}{2}$时,-m2-2m+3=-(-$\frac{3}{2}$)2-2×(-$\frac{3}{2}$)+3=$\frac{15}{4}$,
则此时点E坐标为(-$\frac{3}{2}$,$\frac{15}{4}$);
(3)∵点A和点B关于x轴对称,
∴连接BC交对称轴与点P,
则点P就是使△PAC的周长最小的点,
∵抛物线y=-x2-2x+3的对称轴为x=-1,点P在抛物线的对称轴上,
∴设P(-1,b),
故直线BC的解析式为:y=x+3,
把P(-1,b)代入y=-x+3得b=2,
∴P(-1,2);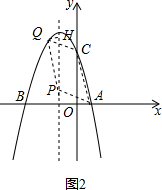
(4)存在,如图2,
设P(-1,b),Q(a,-a2-2a+3),
∵AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∵以A,C,P,Q为顶点的四边形是平行四边形,
∴PQ=AC,PQ∥AC,过Q作QH⊥对称轴于H,
∴∠ACO=∠QPH,
∴△ACO∽△PQH,
∴$\frac{OA}{OC}$=$\frac{QH}{PH}$,
∴$\frac{-a-1}{-{a}^{2}-2a+3-b}=\frac{1}{3}$,
∴b=-a2+a+6,
∵$\sqrt{(-1-a)^{2}+(b+{a}^{2}+2a-3)^{2}}$=$\sqrt{10}$,
∴(1+a)2+(-a2+a+6+a2+2a-3)2=10,
解得:a=0(不合题意舍去),a=-2,
∴Q(-2,3).
∴在抛物线上存在一点Q,使得以A,C,P,Q为顶点的四边形是平行四边形.
点评 本题考查了待定系数法求二次函数的解析式,求最短距离问题,两点间的距离公式,平面直角坐标系中点的坐标与线段长度的关系,利用二次函数求面积的最大值,相似三角形的判定和性质,勾股定理,根据图形得出三角形BEC的面积=三角形BEF的面积+梯形COFE的面积-三角形BOC的面积是解本题第二问的关键.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
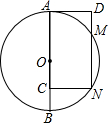 如图,⊙O的直径AB=10,C是AB上一点,矩形ACND交⊙O于M,N两点,若DN=8,则AD的值为( )
如图,⊙O的直径AB=10,C是AB上一点,矩形ACND交⊙O于M,N两点,若DN=8,则AD的值为( )| A. | 4 | B. | 6 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
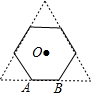 如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.
如图,正三角形的边长为6cm,剪去三个角后成一个正六边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
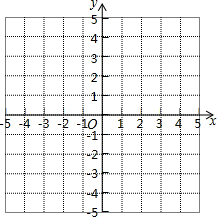 一次函数y1=x-2与二次函数y2=ax2+bx+c的图象交于A(2,m)、B(n,3)两点,且抛物线的对称轴为直线x=3.
一次函数y1=x-2与二次函数y2=ax2+bx+c的图象交于A(2,m)、B(n,3)两点,且抛物线的对称轴为直线x=3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
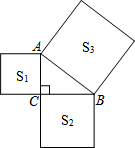 如图,△ABC中,∠ACB=90°,以它的各边为边向外作三个正方形,面积分别为S1,S2,S3,已知S1=15,S3=25,则S2=10.
如图,△ABC中,∠ACB=90°,以它的各边为边向外作三个正方形,面积分别为S1,S2,S3,已知S1=15,S3=25,则S2=10.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com