
分析 连接OC,由勾股定理求出OP,分两种情况即可得出BP的长.
解答 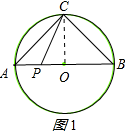 解:连接OC
解:连接OC
∵CA=CB,OA=OB,
∴OC⊥AB,
∴∠AOC=90°,
∵OB=OC=$\frac{1}{2}$AB=3,
∴OP=$\sqrt{C{P}^{2}-O{C}^{2}}$=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$,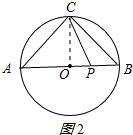 分两种情况:
分两种情况:
①如图1所示:BP=OB+OP=3+$\sqrt{7}$;
②如图2所示:BP=OB-OP=3-$\sqrt{7}$;
综上所述:BP的长为3+$\sqrt{7}$或3-$\sqrt{7}$;
故答案为:3+$\sqrt{7}$或3-$\sqrt{7}$.
点评 本题考查了三角形的外接圆与外心、勾股定理;熟练掌握勾股定理,分两种情况讨论是解决问题的关键.


科目:初中数学 来源: 题型:解答题
| 成绩(分) | 71 | 74 | 78 | 80 | 82 | 83 | 85 | 86 | 88 | 90 | 91 | 92 | 94 |
| 人数 | 1 | 2 | 3 | 5 | 4 | 5 | 3 | 7 | 8 | 4 | 3 | 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
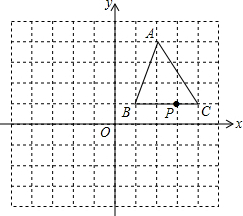 如图,三角形ABC的顶点坐标分别为A(2,4)、B(1,1)、C(4,1).BC上的一点P的坐标为P(3,1),将三角形ABC向左平移4个单位,再向上平移1个单位,得到三角形A1B1C1,其中点A、B、C、P分别对应点A1、B1、C1、P1.
如图,三角形ABC的顶点坐标分别为A(2,4)、B(1,1)、C(4,1).BC上的一点P的坐标为P(3,1),将三角形ABC向左平移4个单位,再向上平移1个单位,得到三角形A1B1C1,其中点A、B、C、P分别对应点A1、B1、C1、P1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
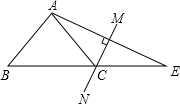 如图,在△ABE中,∠A=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )
如图,在△ABE中,∠A=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )| A. | 45° | B. | 60° | C. | 50° | D. | 55° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com