
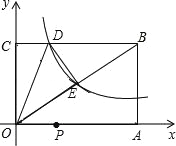
【题目】如图,已知矩形OABC的两边OA、OC分别落在x轴、y轴的正半轴上,顶点B的坐标是(6,4),反比例函数y=![]() (x>0)的图象经过矩形对角线的交点E,且与BC边交于点D.
(x>0)的图象经过矩形对角线的交点E,且与BC边交于点D.
(1)①求反比例函数的解析式与点D的坐标;②直接写出△ODE的面积;
(2)若P是OA上的动点,求使得“PD+PE之和最小”时的直线PE的解析式.
【答案】(1)①D(1.5,4),②4.5;(2)y=﹣4x+10.
【解析】
试题分析:(1)①连接OE,则O、E、三点共线,则E是OB的中点,即可求得E的坐标,利用待定系数法求得函数的解析式,进而求得D的坐标;②根据S△ODE=S△OBC﹣S△OCD﹣S△BDE即可求解;(2)作E关于OA轴的对称点E',则直线DE'就是所求的直线PE,利用待定系数法即可求解.
试题解析:(1)①如图:连接OB,则O、E、B三点共线.∵B的坐标是(6,4),E是矩形对角线的交点,∴E的坐标是(3,2),∴k=3×2=6,则函数的解析式是y=![]() .当y=4时,x=1.5,即D的坐标是(1.5,4);②S△OBC=
.当y=4时,x=1.5,即D的坐标是(1.5,4);②S△OBC=![]() BCOC=
BCOC=![]() ×6×4=12,S△OCD=
×6×4=12,S△OCD=![]() OCCD=
OCCD=![]() ×4×1.5=3,S△BDE=
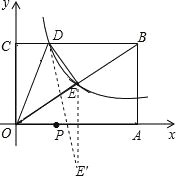
×4×1.5=3,S△BDE=![]() ×(6﹣1.5)×2=4.5,则S△ODE=S△OBC﹣S△OCD﹣S△BDE=12﹣3﹣3﹣4.5=4.5;(2)作E关于OA轴的对称点E',则E'的坐标是(3,﹣2).连接E'D,与x轴交点是P,此时PO+PE最小.设y=mx+n,把E'和D的坐标代入得:
×(6﹣1.5)×2=4.5,则S△ODE=S△OBC﹣S△OCD﹣S△BDE=12﹣3﹣3﹣4.5=4.5;(2)作E关于OA轴的对称点E',则E'的坐标是(3,﹣2).连接E'D,与x轴交点是P,此时PO+PE最小.设y=mx+n,把E'和D的坐标代入得:![]() ,解得:
,解得:![]() ,
,
则直线PE的解析式是y=﹣4x+10.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com