
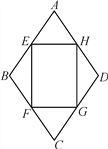
【题目】如图,四边形ABCD是一个菱形绿地,其周长为40![]() m,∠ABC=120°,在其内部有一个四边形花坛EFGH,其四个顶点恰好在菱形ABCD各边的中点,现在准备在花坛中种植茉莉花,其单价为10元/m2,请问需投资金多少元?(结果保留整数)
m,∠ABC=120°,在其内部有一个四边形花坛EFGH,其四个顶点恰好在菱形ABCD各边的中点,现在准备在花坛中种植茉莉花,其单价为10元/m2,请问需投资金多少元?(结果保留整数)
【答案】866元
【解析】分析:连接BD,AC,由菱形ABCD的周长求出边长,再由∠ABC的度数确定出三角形ABD与三角形BCD都为等边三角形,进而求出BD与AC的长,由E、F、G、H分别为中点确定出四边形EFGH为矩形,求出矩形边长,进而求出矩形面积,求出所求即可.
详解:连接BD,AC.
∵菱形ABCD的周长为40![]() m,∴菱形ABCD的边长为10
m,∴菱形ABCD的边长为10![]() m.
m.
∵∠ABC=120°,∴△ABD,△BCD是等边三角形,∴对角线BD=10![]() m,AC=10
m,AC=10![]() m.
m.
∵E,F,G,H是菱形ABCD各边的中点,∴四边形EFGH是矩形,矩形的边长分别为5![]() m,5
m,5![]() m,∴矩形EFGH的面积为5
m,∴矩形EFGH的面积为5![]() ×5
×5![]() =50
=50![]() (m2),即需投资金为50
(m2),即需投资金为50![]() ×10=500
×10=500![]() ≈866(元).
≈866(元).
答:需投资金为866元.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】长方形OABC,O为平面直角坐标系的原点,OA=5,OC=3,点B在第三象限.
(1)求点B的坐标;
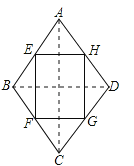
(2)如图1,若过点B的直线BP与长方形OABC的边交于点P,且将长方形OABC的面积分为1:4两部分,求点P的坐标;
(3)如图2,M为x轴负半轴上一点,且∠CBM=∠CMB,N是x轴正半轴上一动点,∠MCN的平分线CD交BM的延长线于点D,在点N运动的过程中,![]() 的值是否变化?若不变,求出其值;若变化,请说明理由.
的值是否变化?若不变,求出其值;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,AB=AC.过A点的直线a从与边AC重合的位置开始绕点A按顺时针方向旋转角θ,直线a交BC边于点P(点P不与点B、点C重合),△BMN的边MN始终在直线a上(点M在点N的上方),且BM=BN,连接CN.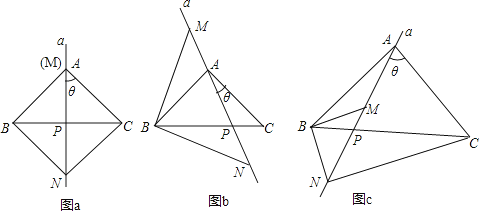
(1)当∠BAC=∠MBN=90°时,
①如图a,当θ=45°时,∠ANC的度数为△;
②如图b,当θ≠45°时,①中的结论是否发生变化?说明理由;
(2)如图c,当∠BAC=∠MBN≠90°时,请直接写出∠ANC与∠BAC之间的数量关系,不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=60°,AC=a,作斜边AB边中线CD,得到第一个三角形ACD;DE⊥BC于点E,作Rt△BDE斜边DB上中线EF,得到第二个三角形DEF;依此作下去…则第n个三角形的面积等于 . 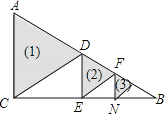
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店以每箱60元新进一批苹果共400箱,为计算总重量,从中任选30箱苹果称重,发现每箱苹果重量都在10千克左右,现以10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,将称重记录如下:
规格 | ﹣0.2 | ﹣0.1 | 0 | 0.1 | 0.2 | 0.5 |
筐数 | 5 | 8 | 2 | 6 | 8 | 1 |
(1)求30箱苹果的总重量
(2)若每千克苹果的售价为10元,则卖完这批苹果共获利多少元
查看答案和解析>>
科目:初中数学 来源: 题型:
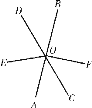
【题目】如图,已知直线AB,CD相交于点O,OE平分∠AOD,FO⊥AB,垂足为O,![]() ∠BOD=∠DOE.
∠BOD=∠DOE.
(1)求∠BOF的度数;
(2)请写出图中与∠BOD相等的所有的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD位于平面直角坐标系的第一象限,B、C在x轴上A点函数![]() 上,且AB∥CD∥y轴,AD∥x轴,B(1,0)、C(3,0)。
上,且AB∥CD∥y轴,AD∥x轴,B(1,0)、C(3,0)。
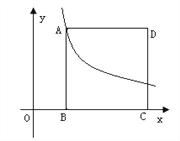
⑴试判断四边形ABCD的形状。
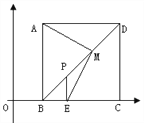
⑵如图若点P是线段BD上一点PE⊥BC于E,M是PD的中点,连EM、AM。
求证:AM=EM
⑶在图中,连结AE交BD于N,则下列两个结论:
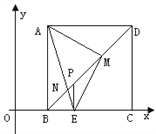
①![]() 值不变;②
值不变;②![]() 的值不变。其中有且仅有一个是正确的,请选择正确的结论证明并求其值。
的值不变。其中有且仅有一个是正确的,请选择正确的结论证明并求其值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解答下面的问题:
我们知道方程![]() 有无数个解,但在实际生活中我们往往只需求出其
有无数个解,但在实际生活中我们往往只需求出其
正整数解.
例:由![]() ,得:
,得:![]() ,(x、y为正整数)
,(x、y为正整数)
∴![]() ,则有
,则有![]() .又
.又![]() 为正整数,则
为正整数,则![]() 为正整数.由2与3互质,可知:x为3的倍数,从而x=3,代入
为正整数.由2与3互质,可知:x为3的倍数,从而x=3,代入![]() ∴2x+3y=12的正整数解为
∴2x+3y=12的正整数解为![]()
问题:
(1)请你写出方程![]() 的一组正整数解: .
的一组正整数解: .
(2)若![]() 为自然数,则满足条件的x值为 .
为自然数,则满足条件的x值为 .
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com