
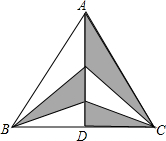
 如图,△ABC中,AD是BC的中垂线,若BC=8,AD=6,则图中阴影部分的面积是12.
如图,△ABC中,AD是BC的中垂线,若BC=8,AD=6,则图中阴影部分的面积是12.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 若a2=b2,则a=b | B. | 若a<b,则$\sqrt{{a}^{2}}<\sqrt{{b}^{2}}$ | C. | 若$\root{3}{a}$=$\root{3}{b}$,则$\sqrt{a}=\sqrt{b}$ | D. | 若a>b,则$\root{3}{a}$$>\root{3}{b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
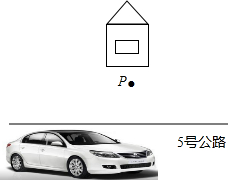 如图所示,一次缉毒行动中,警方获可靠信息,一运毒车将经过5号公路,但由于车上有爆炸装置,警方无法靠近,只能使用远程射击的方法,为了减少对周围的伤亡,警方选中一距离公路120m的隐蔽处P点,射程为200m,准备行动,此时发现,运毒车已经来到与P点的水平距离为300m处,若运毒车的车速为20m/s,那警察发现后要在几秒钟内对其进行射击?
如图所示,一次缉毒行动中,警方获可靠信息,一运毒车将经过5号公路,但由于车上有爆炸装置,警方无法靠近,只能使用远程射击的方法,为了减少对周围的伤亡,警方选中一距离公路120m的隐蔽处P点,射程为200m,准备行动,此时发现,运毒车已经来到与P点的水平距离为300m处,若运毒车的车速为20m/s,那警察发现后要在几秒钟内对其进行射击?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com