
【题目】如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).
(1)求反比例函数的解析式;
(2)反比例函数的图象与线段BC交于点D,直线![]() 过点D,与线段AB相交于点F,求点F的坐标;
过点D,与线段AB相交于点F,求点F的坐标;
(3)连接OF,OE,探究∠AOF与∠EOC的数量关系,并证明.
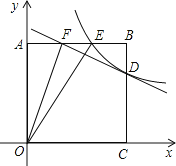
【答案】(1)y=![]() ;(2)点F的坐标为(2,4).(3)∠AOF=∠EOC.见解析
;(2)点F的坐标为(2,4).(3)∠AOF=∠EOC.见解析
【解析】试题分析:(1)设反比例函数的解析式为y=,把点E(3,4)代入即可求出k的值,进而得出结论;
(2)由正方形AOCB的边长为4,故可知点D的横坐标为4,点F的纵坐标为4.由于点D在反比例函数的图象上,所以点D的纵坐标为3,即D(4,3),由点D在直线y=﹣x+b上可得出b的值,进而得出该直线的解析式,再把y=4代入直线的解析式即可求出点F的坐标;
(3)在CD上取CG=AF=2,连接OG,连接EG并延长交x轴于点H,由全等三角形的判定定理可知△OAF≌△OCG,△EGB≌△HGC(ASA),故可得出EG=HG.设直线EG的解析式为y=mx+n,把E(3,4),G(4,2)代入即可求出直线EG的解析式,故可得出H点的坐标,在Rt△AOF中,AO=4,AE=3,根据勾股定理得OE=5,可知OH=OE,即OG是等腰三角形底边EF上的中线.所以OG是等腰三角形顶角的平分线,由此即可得出结论.
解:(1)设反比例函数的解析式y=,
∵反比例函数的图象过点E(3,4),
∴4=,即k=12.
∴反比例函数的解析式y=![]() ;
;
(2)∵正方形AOCB的边长为4,
∴点D的横坐标为4,点F的纵坐标为4.
∵点D在反比例函数的图象上,
∴点D的纵坐标为3,即D(4,3).
∵点D在直线y=﹣x+b上,
∴3=﹣×4+b,解得b=5.
∴直线DF为y=﹣x+5,
将y=4代入y=﹣x+5,得4=﹣x+5,解得x=2.
∴点F的坐标为(2,4).
(3)∠AOF=∠EOC.
证明:在CD上取CG=AF=2,连接OG,连接EG并延长交x轴于点H.
∵AO=CO=4,∠OAF=∠OCG=90°,AF=CG=2,
∴△OAF≌△OCG(SAS).
∴∠AOF=∠COG.
∵∠EGB=∠HGC,∠B=∠GCH=90°,BG=CG=2,
∴△EGB≌△HGC(ASA).
∴EG=HG.
设直线EG:y=mx+n,
∵E(3,4),G(4,2),
∴![]() ,解得,
,解得,![]() .
.
∴直线EG:y=﹣2x+10.
令y=﹣2x+10=0,得x=5.
∴H(5,0),OH=5.
在Rt△AOE中,AO=4,AE=3,根据勾股定理得OE=5.
∴OH=OE.
∴OG是等腰三角形底边EH上的中线.
∴OG是等腰三角形顶角的平分线.
∴∠EOG=∠GOH.
∴∠EOG=∠GOC=∠AOF,即∠AOF=∠EOC.


科目:初中数学 来源: 题型:
【题目】在一次射击练习中,某运动员命中的环数是7,9,9,10,10,其中9是( )
A. 平均数 B. 中位数 C. 众数 D. 既是平均数和中位数,又是众数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年4月,全国山地越野车大赛在我市某区举行,其中8名选手某项得分如表:
得分 | 80 | 85 | 87 | 90 |
人数 | 1 | 3 | 2 | 2 |
则这8名选手得分的众数、中位数分别是( )
A. 85,85 B. 87,85 C. 85,86 D. 85,87
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=5,AC=6,BC=7,点D,E分别在AB,AC上,DE∥BC.
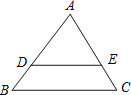
(1)当AD:DB=4:3时,求DE长;
(2)当△ADE的周长与四边形BCED的周长相等,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.
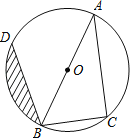
(1)求BD的长;
(2)求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com