
 如图,在△ABC中,AB=BC,∠ABC=x°,将△ABC绕点B顺时针旋转角α(0°<α<x°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点,观察并猜想:在旋转过程中,线段EA1与FC有怎样的数量关系?并证明你的结论.
如图,在△ABC中,AB=BC,∠ABC=x°,将△ABC绕点B顺时针旋转角α(0°<α<x°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点,观察并猜想:在旋转过程中,线段EA1与FC有怎样的数量关系?并证明你的结论.
|


科目:初中数学 来源: 题型:
 如图,P是边长为1的正三角形ABC的BC边上一点,从P向AB引垂线PQ,延长QP与AC延长线交于R.
如图,P是边长为1的正三角形ABC的BC边上一点,从P向AB引垂线PQ,延长QP与AC延长线交于R.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数y=
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
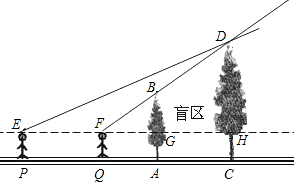 如图,两棵树的高度分别为AB=6m,CD=8m,两树的根部间的距离AC=4m,小强正在距树AB的20m的点P处从左向右前进,如果小强的眼睛与地面的距离为1.6m,当小强前进多少米时,就恰好不能看到CD的树顶D?
如图,两棵树的高度分别为AB=6m,CD=8m,两树的根部间的距离AC=4m,小强正在距树AB的20m的点P处从左向右前进,如果小强的眼睛与地面的距离为1.6m,当小强前进多少米时,就恰好不能看到CD的树顶D?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com