
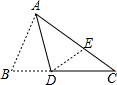
 将△ABC如图折叠,使B点落在AC边上E处,折痕为AD,已知∠B=2∠C,则AB,BD,AC三者之间的关系是AB+BD=AC.
将△ABC如图折叠,使B点落在AC边上E处,折痕为AD,已知∠B=2∠C,则AB,BD,AC三者之间的关系是AB+BD=AC.  智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
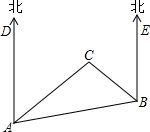 如图,是A、B、C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西30°方向,从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB呢?
如图,是A、B、C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西30°方向,从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB呢?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某养猪专业户利用一堵砖墙(长度足够)围成一个长方形猪栏,围猪栏的栅栏一共长40m,设这个长方形的相邻两边的长分别为x(m)和y(m).
某养猪专业户利用一堵砖墙(长度足够)围成一个长方形猪栏,围猪栏的栅栏一共长40m,设这个长方形的相邻两边的长分别为x(m)和y(m).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 答题情况 | 答对 | 答错或不答 |
| 题数 | x | 25-x |
| 每题分值 | 10 | -5 |
| 得分 | 10x | -5(25-x) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com