
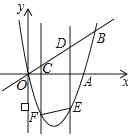
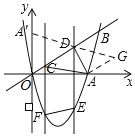
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§y=x2Љ4xЕФЭМЯѓгыxжсЁЂжБЯпy=xЕФвЛИіНЛЕуЗжБ№ЮЊЕуAЁЂBЃЌCDЪЧЯпЖЮOBЩЯЕФвЛЖЏЯпЖЮЃЌЧвCD=2ЃЌЙ§ЕуCЁЂDЕФСНжБЯпЖМЦНаагкyжсЃЌгыХзЮяЯпЯрНЛгкЕуFЁЂEЃЌСЌНгEFЃЎ
ЃЈ1ЃЉЕуAЕФзјБъЮЊЁЁ ЁЁЃЌЯпЖЮOBЕФГЄ=ЁЁ ЁЁЃЛ
ЃЈ2ЃЉЩшЕуCЕФКсзјБъЮЊmЃЎ
ЂйЕБЫФБпаЮCDEFЪЧЦНааЫФБпаЮЪБЃЌЧѓmЕФжЕЃЛ
ЂкСЌНгACЁЂADЃЌЧѓmЮЊКЮжЕЪБЃЌЁїACDЕФжмГЄзюаЁЃЌВЂЧѓГіетИізюаЁжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ AЃЈ4ЃЌ0ЃЉЃЌ5![]() ЃЛЃЈ2ЃЉЂй
ЃЛЃЈ2ЃЉЂй![]() ЃЛЂкЕБm=
ЃЛЂкЕБm=![]() ЪБЃЌЁїACDЕФжмГЄзюаЁЃЌетИізюаЁжЕЮЊ8ЃЎ
ЪБЃЌЁїACDЕФжмГЄзюаЁЃЌетИізюаЁжЕЮЊ8ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнy=x2Љ4xжаЃЌСюy=0ЃЌдђ0=x2Љ4xЃЌПЩЧѓЕУAЃЈ4ЃЌ0ЃЉЃЌНтЗНГЬзщ![]() ЃЌПЩЕУBЃЈ5ЃЌ5ЃЉЃЌНјЖјЕУГіOBЕФГЄЃЛ
ЃЌПЩЕУBЃЈ5ЃЌ5ЃЉЃЌНјЖјЕУГіOBЕФГЄЃЛ
ЃЈ2ЃЉЂйИљОнCЃЈmЃЌmЃЉЃЌFЃЈmЃЌm2Љ4mЃЉЃЌПЩЕУCF=mЉЃЈm2Љ4mЃЉЃЌИљОнDЃЈm![]() ЃЌm
ЃЌm![]() ЃЉЃЌEЃЈm
ЃЉЃЌEЃЈm![]() ЃЌЃЈm
ЃЌЃЈm![]() ЃЉ2Љ4ЃЈm
ЃЉ2Љ4ЃЈm![]() ЃЉЃЉЃЌПЩЕУDE=m
ЃЉЃЉЃЌПЩЕУDE=m![]() [ЃЈm
[ЃЈm![]() ЃЉ2Љ4ЃЈm
ЃЉ2Љ4ЃЈm![]() ЃЉ]ЃЌзюКѓИљОнЕБЫФБпаЮCDEFЪЧЦНааЫФБпаЮЪБЃЌCF=DEЃЌЧѓЕУmЕФжЕМДПЩЃЛ
ЃЉ]ЃЌзюКѓИљОнЕБЫФБпаЮCDEFЪЧЦНааЫФБпаЮЪБЃЌCF=DEЃЌЧѓЕУmЕФжЕМДПЩЃЛ
ЂкЯШЙ§ЕуAзїCDЕФЦНааЯпЃЌЙ§ЕуDзїACЕФЦНааЯпЃЌНЛгкЕуGЃЌдђЫФБпаЮACDGЪЧЦНааЫФБпаЮЃЌЕУГіAC=DGЃЌдйзїЕуAЙигкжБЯпOBЕФЖдГЦЕуA'ЃЌСЌНгA'DЃЌдђA'D=ADЃЌИљОнЕБA'ЃЌDЃЌGШ§ЕуЙВЯпЪБЃЌA'D+DG=A'GзюЖЬЃЌПЩЕУДЫЪБAC+ADзюЖЬЃЌШЛКѓЧѓЕУжБЯпA'GЕФНтЮіЪНЮЊy![]() x+4ЃЌНтЗНГЬзщПЩЕУDЁЂCЕФзјБъЃЌзюКѓИљОнСНЕуМфОрРыЙЋЪНЃЌЧѓЕУЁїACDЕФжмГЄЕФзюаЁжЕЃЎ
x+4ЃЌНтЗНГЬзщПЩЕУDЁЂCЕФзјБъЃЌзюКѓИљОнСНЕуМфОрРыЙЋЪНЃЌЧѓЕУЁїACDЕФжмГЄЕФзюаЁжЕЃЎ
ЃЈ1ЃЉЁпy=x2Љ4xжаЃЌСюy=0ЃЌдђ0=x2Љ4xЃЌ
НтЕУЃКx1=0ЃЌx2=4ЃЌ
ЁрAЃЈ4ЃЌ0ЃЉЃЌНтЗНГЬзщ![]() ЃЌ
ЃЌ
ПЩЕУЃК![]() Лђ
Лђ![]() ЃЌ
ЃЌ
ЁрBЃЈ5ЃЌ5ЃЉЃЌ
ЁрOB![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃКЃЈ4ЃЌ0ЃЉЃЌ5![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйЁпЕуCЕФКсзјБъЮЊmЃЌЧвCFЁЮDEЁЮyжсЃЌ
ЁрCЃЈmЃЌmЃЉЃЌFЃЈmЃЌm2Љ4mЃЉЃЎ
гжЁпCD=2ЃЌЧвCDЪЧЯпЖЮOBЩЯЕФвЛЖЏЯпЖЮЃЌ
ЁрDЃЈm![]() ЃЌm
ЃЌm![]() ЃЉЃЌEЃЈm
ЃЉЃЌEЃЈm![]() ЃЌЃЈm
ЃЌЃЈm![]() ЃЉ2Љ4ЃЈm
ЃЉ2Љ4ЃЈm![]() ЃЉЃЉЃЌ
ЃЉЃЉЃЌ
ЁрCF=mЉЃЈm2Љ4mЃЉЃЌDE=m![]() [ЃЈm
[ЃЈm![]() ЃЉ2Љ4ЃЈm
ЃЉ2Љ4ЃЈm![]() ЃЉ]ЃЎ
ЃЉ]ЃЎ
ЁпЕБЫФБпаЮCDEFЪЧЦНааЫФБпаЮЪБЃЌCF=DEЃЌ
ЁрmЉЃЈm2Љ4mЃЉ=m![]() [ЃЈm
[ЃЈm![]() ЃЉ2Љ4ЃЈm
ЃЉ2Љ4ЃЈm![]() ЃЉ]ЃЌ
ЃЉ]ЃЌ
НтЕУЃК![]() ЃЛ
ЃЛ
ЂкШчЭМЫљЪОЃЌЙ§ЕуAзїCDЕФЦНааЯпЃЌЙ§ЕуDзїACЕФЦНааЯпЃЌНЛгкЕуGЃЌдђЫФБпаЮACDGЪЧЦНааЫФБпаЮЃЌ
ЁрAC=DGЃЌ
зїЕуAЙигкжБЯпOBЕФЖдГЦЕуA'ЃЌСЌНгA'DЃЌдђA'D=ADЃЌ
ЁрЕБA'ЃЌDЃЌGШ§ЕуЙВЯпЪБЃЌA'D+DG=A'GзюЖЬЃЌДЫЪБAC+ADзюЖЬЃЎ
ЁпAЃЈ4ЃЌ0ЃЉЃЌAG=CD=2ЃЌ
ЁрA'ЃЈ0ЃЌ4ЃЉЃЌGЃЈ4![]() ЃЉЃЌ
ЃЉЃЌ
ЩшжБЯпA'GЕФНтЮіЪНЮЊy=kx+bЃЌдђ![]() ЃЌ
ЃЌ
НтЕУЃК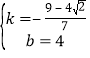 ЃЌ
ЃЌ
ЁржБЯпA'GЕФНтЮіЪНЮЊy![]() x+4ЃЌ
x+4ЃЌ
НтЗНГЬзщ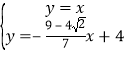 ЃЌ
ЃЌ
ПЩЕУЃК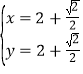 ЃЌ
ЃЌ
ЁрDЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁпCD=2ЃЌЧвCDЪЧЯпЖЮOBЩЯЕФвЛЖЏЯпЖЮЃЌ
ЁрCЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрЕуCЕФКсзјБъm=![]() ЃЎ
ЃЎ
ЁпAD=A'DЃЌAC=DGЃЌCD=AG=2ЃЌ
ЁрЁїACDЕФзюаЁжЕЮЊA'G+AG=![]() =6+2=8ЃЌ
=6+2=8ЃЌ
ЙЪЕБm=![]() ЪБЃЌЁїACDЕФжмГЄзюаЁЃЌетИізюаЁжЕЮЊ8ЃЎ
ЪБЃЌЁїACDЕФжмГЄзюаЁЃЌетИізюаЁжЕЮЊ8ЃЎ


 ГіВЪЭЌВНДѓЪдОэЯЕСаД№АИ
ГіВЪЭЌВНДѓЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЖЅЕузјБъ
ЃЌЖЅЕузјБъ![]() ЧвПЊПкЯђЯТЃЌдђЯТСаНсТлЃКЂйХзЮяЯпОЙ§Еу
ЧвПЊПкЯђЯТЃЌдђЯТСаНсТлЃКЂйХзЮяЯпОЙ§Еу![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂлЙигк
ЃЛЂлЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЛЂмЖдгкШЮвтЪЕЪ§
гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЛЂмЖдгкШЮвтЪЕЪ§![]() ЃЌ
ЃЌ![]() змГЩСЂЁЃЦфжаНсТле§ШЗЕФИіЪ§ЮЊЃЈ ЃЉ
змГЩСЂЁЃЦфжаНсТле§ШЗЕФИіЪ§ЮЊЃЈ ЃЉ
A. 1ИіB. 2ИіC. 3ИіD. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦьИЫABЕФЖЅЖЫBдкЯІбєЕФгрЛдЯТТфдквЛИіаБЦТЩЯЕФЕуDДІЃЌФГаЃЪ§бЇПЮЭтаЫШЄаЁзщЕФЭЌбЇе§дкВтСПЦьИЫЕФИпЖШЃЌдкЦьИЫЕФЕзВПAДІВтЕУЕуDЕФбіНЧЮЊ15ЁуЃЌAC=10УзЃЌгжВтЕУЁЯBDA=45ЁуЃЎвбжЊаБЦТCDЕФЦТЖШЮЊi=1ЃК![]() ЃЌЧѓЦьИЫABЕФИпЖШЃЈ
ЃЌЧѓЦьИЫABЕФИпЖШЃЈ![]() Ёж1.7ЃЌНсЙћОЋШЗЕНИіЮЛЃЉЃЎ
Ёж1.7ЃЌНсЙћОЋШЗЕНИіЮЛЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дкЁїABCжа,ЁЯACB=100Ёу,AC=AE,BC=BD,дђЁЯDCEЕФЖШЪ§ЮЊ
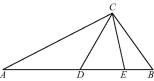
A. 20Ёу B. 25Ёу C. 30Ёу D. 40Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫНтбЇЩњЖдЁАЕкЖўЪЎНьжаЙњЙўЖћБѕБљбЉДѓЪРНчЁБжїЬтОАЙлЕФСЫНтЧщПі,дкШЋЬхбЇЩњжаЫцЛњГщШЁСЫВПЗжбЇЩњНјааЕїВщ,ВЂАбЕїВщНсЙћЛцжЦГЩШчЭМЕФВЛЭъећЕФСНЗљЭГМЦЭМ:
(1)БОДЮЕїВщЙВГщШЁСЫЖрЩйУћбЇЩњЃЛ
(2)ЭЈЙ§МЦЫуВЙШЋЬѕаЮЭМЃЛ
(3)ШєИУбЇаЃЙВга![]() УћбЇЩњ,ЧыФуЙРМЦИУбЇаЃбЁдёЁАБШНЯСЫНтЁБЯюФПЕФбЇЩњгаЖрЩйУћЃП
УћбЇЩњ,ЧыФуЙРМЦИУбЇаЃбЁдёЁАБШНЯСЫНтЁБЯюФПЕФбЇЩњгаЖрЩйУћЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
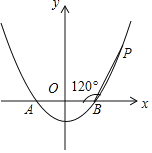
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯп![]() гыxжсЯрНЛгкAЃЌBСНЕуЃЌЕуPЪЧХзЮяЯпЩЯвЛЕуЃЌЧв
гыxжсЯрНЛгкAЃЌBСНЕуЃЌЕуPЪЧХзЮяЯпЩЯвЛЕуЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
![]() ЧѓИУХзЮяЯпЕФБэДяЪНЃЛ
ЧѓИУХзЮяЯпЕФБэДяЪНЃЛ
![]() ЩшЕу
ЩшЕу![]() ЮЊХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЕБЕуMдкЧњЯпBAжЎМф
ЮЊХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЕБЕуMдкЧњЯпBAжЎМф![]() КЌЖЫЕу
КЌЖЫЕу![]() вЦЖЏЪБЃЌЧѓ
вЦЖЏЪБЃЌЧѓ![]() ЕФзюДѓжЕМАШЁЕУзюДѓжЕЪБЕуMЕФзјБъЃЎ
ЕФзюДѓжЕМАШЁЕУзюДѓжЕЪБЕуMЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
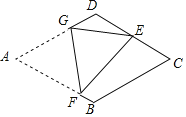
ЁОЬтФПЁПШчЭМЃЌдкСтаЮжНЦЌABCDжаЃЌABЃН4ЃЌЁЯAЃН60ЁуЃЌНЋСтаЮжНЦЌЗелЃЌЪЙЕуAТфдкCDЕФжаЕуEДІЃЌелКлЮЊFGЃЌЕуFЁЂGЗжБ№дкБпABЁЂADЩЯЃЎдђsinЁЯEFGЕФжЕЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
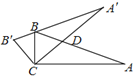
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯACBЃН90ЁуЃЌЁЯAЃН20ЁуЃЎНЋЁїABCШЦЕуCАДФцЪБеыЗНЯђа§зЊЕУЁїAЁфBЁфCЃЌЧвЕуBдкAЁфBЁф ЩЯЃЌCAЁф НЛABгкЕуDЃЌдђЁЯBDCЕФЖШЪ§ЮЊЃЈ ЃЉ
A. 40ЁуB. 50ЁуC. 60ЁуD. 70Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
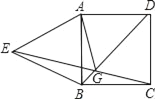
ЁОЬтФПЁПШчЭМЫљЪОЃЌдке§ЗНаЮABCDжаЃЌвдABЮЊБпЯђе§ЗНаЮЭтзїЕШБпШ§НЧаЮABEЃЌСЌНгCEЁЂBDНЛгкЕуGЃЌСЌНгAGЃЌФЧУДЁЯAGDЕФЕзЪ§ЪЧ______ЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com