练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，∠ACB＝90°，∠A＝20°．将△ABC绕点C按逆时针方向旋转得△A′B′C，且点B在A′B′ 上，CA′ 交AB于点D，则∠BDC的度数为（ ）

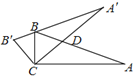
    A. 40°B. 50°C. 60°D. 70°

    【答案】C

    【解析】

    根据旋转的性质可得∠A=∠A′=20°，CB=CB′，则∠CBA=∠B′=90°-20°=70°．根据等腰三角形的性质可得∠CBB′=∠B′=70°，利用平角定义可求出∠A′BD的度数，由外角性质即可得∠BDC的度数.

    ∵将△ABC绕点C按逆时针方向旋转得△A′B′C，∠A=20°，∠ACB=90°，

    ∴∠A=∠A′=20°，CB=CB′，

    ∴∠CBA=∠B′=90°-20°=70°，

    ∴∠CBB′=∠B′=70°，

    ∴∠A′BD=180°-∠CBB′-∠CBA=180°-70°-70°=40°，

    ∴∠BDC=∠A′+∠A′BD=20°+40°=60°，

    故选C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】若直线y=2x+t﹣3与函数y=的图象有且只有两个公共点时，则t的取值范围是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

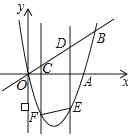
    【题目】如图，二次函数y=x2﹣4x的图象与x轴、直线y=x的一个交点分别为点A、B，CD是线段OB上的一动线段，且CD=2，过点C、D的两直线都平行于y轴，与抛物线相交于点F、E，连接EF．

    （1）点A的坐标为　 　，线段OB的长=　 　；

    （2）设点C的横坐标为m．

    ①当四边形CDEF是平行四边形时，求m的值；

    ②连接AC、AD，求m为何值时，△ACD的周长最小，并求出这个最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

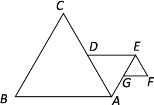
    【题目】如图，作等边△ABC，取AC的中点D，以AD为边向△ABC形外作等边△ADE，取AE的中点G，再以EG为边作等边△EFG，如此反复，当作出第6个三角形时，若AB=4，整个图形的外围周长是______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

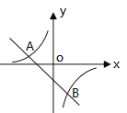
    【题目】如图，一次函数y=kx+b的图象与反比例函数y=图象交于A(－2，1)、B(1，n)两点.

    (1)求反比例函数和一次函数的解析式；

    (2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，AD=BC，∠A=∠B，E为AB的中点，连结CE，DE.

    （1）求证：△ADE≌△BCE.

    （2）若∠A＝70°，∠BCE＝60°，求∠CDE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A、B在双曲线y=(x<0)上，连接OA、AB，以OA、AB为边作□OABC．若点C恰落在双曲线y=(x>0)上，此时□OABC的面积为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“一带一路”的战略构想为国内许多企业的发展带来了新的机遇，某公司生产A，B两种机械设备，每台B种设备的成本是A种设备的1.5倍，公司若投入16万元生产A种设备，36万元生产B种设备，则可生产两种设备共10台．请解答下列问题：

    (1)A、B两种设备每台的成本分别是多少万元？

    (2)若A，B两种设备每台的售价分别是6万元，10万元，公司决定生产两种设备共60台，计划销售后获利不低于126万元，且A种设备至少生产53台，求该公司有几种生产方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】从甲地到乙地有两条公路，一条是全长600km的普通公路，另一条是全长480km的高速公路，某客车在高速公路上行驶的平均速度比在普通公路上快45/ ，由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半，求该客车由高速公路从甲地到乙地所需的时间．

    查看答案和解析>>

    同步练习册答案