
【题目】“一带一路”的战略构想为国内许多企业的发展带来了新的机遇,某公司生产A,B两种机械设备,每台B种设备的成本是A种设备的1.5倍,公司若投入16万元生产A种设备,36万元生产B种设备,则可生产两种设备共10台.请解答下列问题:
(1)A、B两种设备每台的成本分别是多少万元?
(2)若A,B两种设备每台的售价分别是6万元,10万元,公司决定生产两种设备共60台,计划销售后获利不低于126万元,且A种设备至少生产53台,求该公司有几种生产方案.
【答案】(1)A种设备每台的成本是4万元,B种设备每台的成本是6万元;(2)该公司有5种生产方案.
【解析】
(1)设A种设备每台的成本是x万元,B种设备每台的成本是1.5x万元.根据数量=总价÷单价,结合“投入16万元生产A种设备,36万元生产B种设备,则可生产两种设备共10台”,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设A种设备生产a台,则B种设备生产(60﹣a)台.根据销售后获利不低于126万元且A种设备至少生产53台,即可得出关于a的一元一次不等式组,解之即可得出a的取值范围,再根据a为正整数即可得出a的值,进而即可得出该公司生产方案种数;
解:(1)设A种设备每台的成本是x万元,B种设备每台的成本是1.5x万元,
根据题意得:![]() =10,
=10,
解得:x=4,
经检验x=4是分式方程的解,
∴1.5x=6.
答:A种设备每台的成本是4万元,B种设备每台的成本是6万元;
(2)设A种设备生产a台,则B种设备生产(60﹣a)台,
根根据题意得:![]() ,
,
解得:53≤a≤57.
∵a为整数,∴a=53,54,55,56,57,
∴该公司有5种生产方案.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=20°.将△ABC绕点C按逆时针方向旋转得△A′B′C,且点B在A′B′ 上,CA′ 交AB于点D,则∠BDC的度数为( )
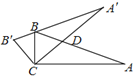
A. 40°B. 50°C. 60°D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
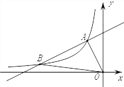
【题目】如图,一次函数y=k1x+b的图象与反比例函数y=![]() (x<0)的图象相交于点A(-1,2)、点B(-4,n).
(x<0)的图象相交于点A(-1,2)、点B(-4,n).
(1)求此一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)在x轴上存在一点P,使△PAB的周长最小,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
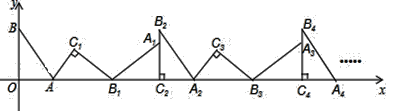
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B,O分别落在点B1,C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(3,0),B(0,4),则点B2018的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
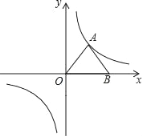
【题目】如图,在反比例函数图象中,△AOB是等边三角形,点A在双曲线的一支上,将△AOB绕点O顺时针旋转α (0°<α<360° ),使点A仍在双曲线上,则α=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
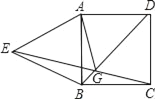
【题目】如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE,连接CE、BD交于点G,连接AG,那么∠AGD的底数是______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
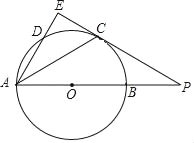
【题目】如图,以AB为直径的⊙O经过点C,过点C作⊙O的切线交AB的延长线于点P,D是⊙O上于点,且弧BC=弧CD,弦AD的延长线交切线PC于点E,连接AC.
(1)求∠E的度数;
(2)若⊙O的直径为5,sinP=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
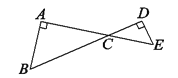
【题目】已知∠A=Rt∠,AB=4,AE=2![]() ,点C在线段AE上运动(不与点A点E重合),过点E作ED⊥BC交BC的延长线于D,则
,点C在线段AE上运动(不与点A点E重合),过点E作ED⊥BC交BC的延长线于D,则![]() 的最大值为( )
的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com