
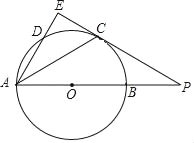
【题目】如图,以AB为直径的⊙O经过点C,过点C作⊙O的切线交AB的延长线于点P,D是⊙O上于点,且弧BC=弧CD,弦AD的延长线交切线PC于点E,连接AC.
(1)求∠E的度数;
(2)若⊙O的直径为5,sinP=![]() ,求AE的长.
,求AE的长.
【答案】(1)90°;(2)4
【解析】
(1)连接OC,根据等腰三角形的性质得到∠OAC=∠OCA,∠OAC=∠CAD,推出OC∥AE,根据平行线的性质得到∠E=∠OCP.根据切线的性质即可得到结论;
(2)运用三角函数值在Rt△OCP中求得OP,然后在Rt△APE中求得AE即可.
解:(1)连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵弧BC=弧CD,
∴∠OAC=∠CAD,
∴∠OCA=∠CAD,
∴OC∥AE,
∴∠E=∠OCP,
∵PE是的切线,C为切点,
∴∠OCP=90°.
∴∠E=90°;
(2)在Rt△OCP中,OC=![]() =2.5,sin∠P=
=2.5,sin∠P=![]() ,
,
∴OP=![]() ,
,
在Rt△APE中,AP=![]() +2.5=
+2.5=![]() ,sin∠P=
,sin∠P=![]() ,
,
∴AE=4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
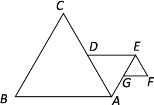
【题目】如图,作等边△ABC,取AC的中点D,以AD为边向△ABC形外作等边△ADE,取AE的中点G,再以EG为边作等边△EFG,如此反复,当作出第6个三角形时,若AB=4,整个图形的外围周长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”的战略构想为国内许多企业的发展带来了新的机遇,某公司生产A,B两种机械设备,每台B种设备的成本是A种设备的1.5倍,公司若投入16万元生产A种设备,36万元生产B种设备,则可生产两种设备共10台.请解答下列问题:
(1)A、B两种设备每台的成本分别是多少万元?
(2)若A,B两种设备每台的售价分别是6万元,10万元,公司决定生产两种设备共60台,计划销售后获利不低于126万元,且A种设备至少生产53台,求该公司有几种生产方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
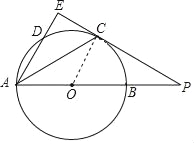
【题目】如图,AB是圆O的直径,点C、D在圆O上,且AD平分∠CAB.过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F.
求证:EF与圆O相切.

查看答案和解析>>
科目:初中数学 来源: 题型:
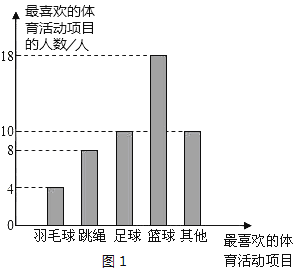
【题目】某校围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据,如图1是根据这组数据绘制的条形统计图,请结合统计图回答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢足球活动的有多少人?占被调查人数的百分比是多少?
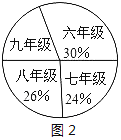
(3)若该校九年级共有400名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢篮球活动的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地有两条公路,一条是全长600km的普通公路,另一条是全长480km的高速公路,某客车在高速公路上行驶的平均速度比在普通公路上快45![]() /
/![]() ,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需的时间.
,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,则下列结论中①BC=BD=AD;②S△ABD:S△BCD=AD:DC;③BC2=CDAC;④若AB=2,则BC=![]() ﹣1,其中正确的结论的个数是_____个.
﹣1,其中正确的结论的个数是_____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为每小时30海里,在此航行过程中,问该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com