
【题目】在半径等于5cm的圆内有长为5![]() cm的弦,则此弦所对的圆周角为( )
cm的弦,则此弦所对的圆周角为( )
A.120° B.30°或120°
C.60° D.60°或120°
【答案】D.
【解析】
试题解析:根据题意画出相应的图形为:
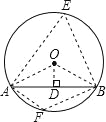
连接OA,OB,在优弧AB上任取一点E,连接AE,BE,在劣弧AB上任取一点F,连接AF,BF,
过O作OD⊥AB,则D为AB的中点,
∵AB=5![]() cm,∴AD=BD=
cm,∴AD=BD=![]() cm,
cm,
又OA=OB=5,OD⊥AB,
∴OD平分∠AOB,即∠AOD=∠BOD=![]() ∠AOB,
∠AOB,
∴在直角三角形AOD中,
sin∠AOD=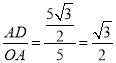 ,
,
∴∠AOD=60°,
∴∠AOB=120°,
又圆心角∠AOB与圆周角∠AEB所对的弧都为![]() ,
,
∴∠AEB=![]() ∠AOB=60°,
∠AOB=60°,
∵四边形AEBF为圆O的内接四边形,
∴∠AFB+∠AEB=180°,
∴∠AFB=180°-∠AEB=120°,
则此弦所对的圆周角为60°或120°.
故选D.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
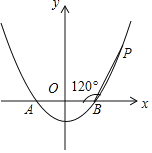
【题目】如图,已知抛物线![]() 与x轴相交于A,B两点,点P是抛物线上一点,且
与x轴相交于A,B两点,点P是抛物线上一点,且![]() ,
,![]() .
.
![]() 求该抛物线的表达式;
求该抛物线的表达式;
![]() 设点
设点![]() 为抛物线上的一个动点,当点M在曲线BA之间
为抛物线上的一个动点,当点M在曲线BA之间![]() 含端点
含端点![]() 移动时,求
移动时,求![]() 的最大值及取得最大值时点M的坐标.
的最大值及取得最大值时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
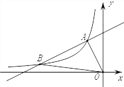
【题目】如图,一次函数y=k1x+b的图象与反比例函数y=![]() (x<0)的图象相交于点A(-1,2)、点B(-4,n).
(x<0)的图象相交于点A(-1,2)、点B(-4,n).
(1)求此一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)在x轴上存在一点P,使△PAB的周长最小,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在反比例函数图象中,△AOB是等边三角形,点A在双曲线的一支上,将△AOB绕点O顺时针旋转α (0°<α<360° ),使点A仍在双曲线上,则α=_____.
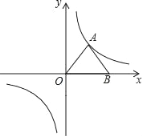
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE,连接CE、BD交于点G,连接AG,那么∠AGD的底数是______度.
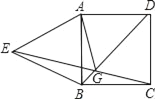
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖为班级联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分 成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘 A 转出了红色,转盘 B 转出 了蓝色,那么配成了紫色.
(1)利用树状图或列表的方法计算配成紫色的概率.
(2)小红和小亮参加这个游戏,并约定配成紫色小红赢,两个转盘转出同种颜色,小亮赢.这个约定对双方公平吗?说明理由.
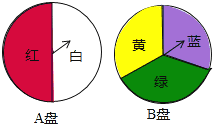
查看答案和解析>>
科目:初中数学 来源: 题型:
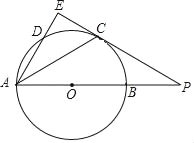
【题目】如图,以AB为直径的⊙O经过点C,过点C作⊙O的切线交AB的延长线于点P,D是⊙O上于点,且弧BC=弧CD,弦AD的延长线交切线PC于点E,连接AC.
(1)求∠E的度数;
(2)若⊙O的直径为5,sinP=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
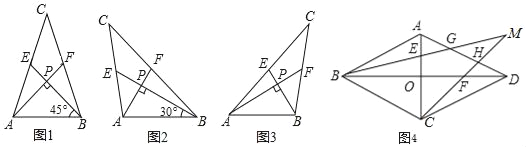
【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P.像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
特例探索
(1)①如图1,当∠ABE=45°,c=2![]() 时,a= ,b= ;
时,a= ,b= ;
②如图2,当∠ABE=30°,c=4时,求a和b的值.
归纳证明
(2)请你观察(1)中的计算结果,猜想三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.
(3)利用(2)中的结论,解答下列问题:
在边长为3的菱形ABCD中,O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连接BE,CF并延长交于点M,BM,CM分别交AD于点G,H,如图4所示,求MG2+MH2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).

(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移![]() 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com