
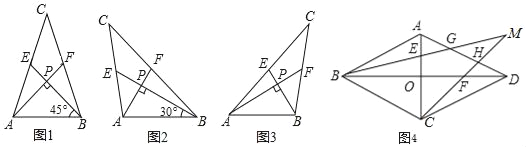
【题目】我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P.像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
特例探索
(1)①如图1,当∠ABE=45°,c=2![]() 时,a= ,b= ;
时,a= ,b= ;
②如图2,当∠ABE=30°,c=4时,求a和b的值.
归纳证明
(2)请你观察(1)中的计算结果,猜想三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式.
(3)利用(2)中的结论,解答下列问题:
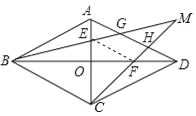
在边长为3的菱形ABCD中,O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连接BE,CF并延长交于点M,BM,CM分别交AD于点G,H,如图4所示,求MG2+MH2的值.
【答案】(1)①2![]() ,2
,2![]() ;② a=2
;② a=2![]() ,b=2
,b=2![]() ;(2)关系为:a2+b2=5c2,证明见解析;(3)5.
;(2)关系为:a2+b2=5c2,证明见解析;(3)5.
【解析】
(1)在图1中,PB=ABsin45°=2=PA,即可求解;同理可得:a=2![]() ,b=2
,b=2![]() ;
;
(2)PB=ABcosα=ccosα,PA=csinα,PF=![]() PA=
PA=![]() csinα,PE=
csinα,PE=![]() csinα,则a2+b2=(2AE)2+(2BF)2,即可求解;
csinα,则a2+b2=(2AE)2+(2BF)2,即可求解;
(3)证明:MG=![]() ME=
ME=![]() MB,MH=
MB,MH=![]() MC,则MG2+MH2=
MC,则MG2+MH2=![]() (MB2+MC2),即可求解.
(MB2+MC2),即可求解.
解:如图1、2、3、4,连接EF,则EF是△ABC的中位线,
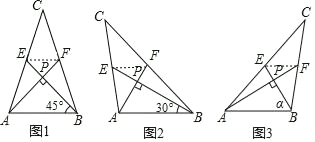
则EF=AB,EF∥AB,∴△EFP∽△BPA,
∴![]() …①,
…①,
(1)在图1中,PB=ABsin45°=2=PA,
由①得:PF=1,
b=2BF=2![]() =2
=2![]() =a;
=a;
②同理可得:a=2![]() ,b=2
,b=2![]() ;
;
(2)关系为:a2+b2=5c2,
证明:如图3,设:∠EAB=α,
则:PB=ABcosα=ccosα,PA=csinα,
由①得:PF=![]() PA=
PA=![]() csinα,PE=
csinα,PE=![]() csinα,
csinα,
则a2+b2=(2AE)2+(2BF)2=c2×5[(sinα)2+(cosα)2]=5c2;
(3)∵AE=OE=![]() EC,AG∥BC,
EC,AG∥BC,
∴AG=![]() BC=
BC=![]() AD,则EF=
AD,则EF=![]() BC=
BC=![]() AD,
AD,
同理HG=![]() AD,∴GH=
AD,∴GH=![]() AD,
AD,
∴GH=![]() EF,
EF,
∵GH∥BC,EF∥BC,
∴HG∥EF,∴MG=![]() ME=
ME=![]() MB,
MB,
同理:MH=![]() MC,
MC,
则MG2+MH2=![]() (MB2+MC2)=
(MB2+MC2)=![]() ×5×BC2=5.
×5×BC2=5.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD=BC,∠A=∠B,E为AB的中点,连结CE,DE.
(1)求证:△ADE≌△BCE.
(2)若∠A=70°,∠BCE=60°,求∠CDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
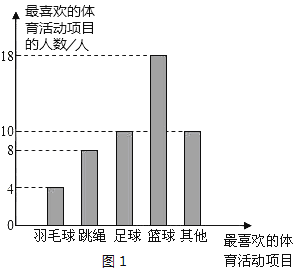
【题目】某校围绕着“你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行了随机抽样调查,从而得到一组数据,如图1是根据这组数据绘制的条形统计图,请结合统计图回答下列问题:
(1)该校对多少名学生进行了抽样调查?
(2)本次抽样调查中,最喜欢足球活动的有多少人?占被调查人数的百分比是多少?
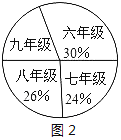
(3)若该校九年级共有400名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢篮球活动的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地有两条公路,一条是全长600km的普通公路,另一条是全长480km的高速公路,某客车在高速公路上行驶的平均速度比在普通公路上快45![]() /
/![]() ,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需的时间.
,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
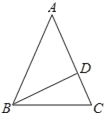
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,则下列结论中①BC=BD=AD;②S△ABD:S△BCD=AD:DC;③BC2=CDAC;④若AB=2,则BC=![]() ﹣1,其中正确的结论的个数是_____个.
﹣1,其中正确的结论的个数是_____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
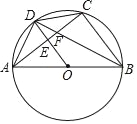
【题目】如图,AB是⊙O的直径,点C是圆上任意一点,点D是AC中点,OD交AC于点E,BD交AC于点F,若BF=1.25DF,则tan∠ABD的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水产养殖户进行小龙虾养殖已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价![]() 元
元![]() 千克
千克![]() 与时间第
与时间第![]() 天
天![]() 之间的函数关系为
之间的函数关系为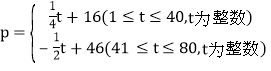 ,日销售量
,日销售量![]() 千克
千克![]() 与时问第
与时问第![]() 天
天![]() 之间的函数关系如图所示.
之间的函数关系如图所示.
![]() 求日销售量y与时间t的函数关系式;
求日销售量y与时间t的函数关系式;
![]() 求利润w与时间t的函数关系式;
求利润w与时间t的函数关系式;
![]() 哪一天的日销售利润最大?最大利润是多少?
哪一天的日销售利润最大?最大利润是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com