
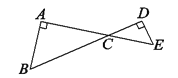
【题目】已知∠A=Rt∠,AB=4,AE=2![]() ,点C在线段AE上运动(不与点A点E重合),过点E作ED⊥BC交BC的延长线于D,则
,点C在线段AE上运动(不与点A点E重合),过点E作ED⊥BC交BC的延长线于D,则![]() 的最大值为( )
的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
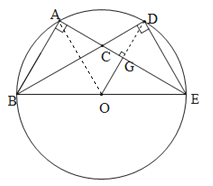
连接BE,作BE的中点O,连接OA、OD.由直角三角形斜边上的中线等于斜边的一半得到OA=OB=OE,OD=OB=OE,从而得到A、B、E、D四点在⊙O上,过O作OG⊥AE于G,延长OG交⊙O于D,则此时DG最大.易证△ABC∽△GDC,得到![]() ,故当DG最大时,
,故当DG最大时,![]() 最大.在Rt△ABE中,利用勾股定理求出BE的长,得到半径的长.由三角形中位线得到OG的长,从而得到DG的最大长度,即可得到结论.
最大.在Rt△ABE中,利用勾股定理求出BE的长,得到半径的长.由三角形中位线得到OG的长,从而得到DG的最大长度,即可得到结论.
连接BE,作BE的中点O,连接OA、OD.
∵∠A=∠BDE=90°,AO是Rt△ABE斜边上的中线,∴OA=OB=OE,同理OD=OB=OE,∴A、B、E、D四点在⊙O上,过O作OG⊥AE于G,延长OG交⊙O于D,则此时DG最大.
∵∠A=90°,∴∠A=∠DGC=90°.
∵∠ACB=∠DCG,∴△ABC∽△GDC,∴![]() ,∴当DG最大时,
,∴当DG最大时,![]() 最大.
最大.
∵BE=![]() =10,∴OB=OE=OD=5.
=10,∴OB=OE=OD=5.
∵OG⊥AE,∴AG=GE.
∵BO=EO,∴OG为△ABE的中位线,∴OG=![]() AB=2,∴DG=OD-OG=5-2=3,∴
AB=2,∴DG=OD-OG=5-2=3,∴![]() .
.
故选C.


科目:初中数学 来源: 题型:
【题目】“一带一路”的战略构想为国内许多企业的发展带来了新的机遇,某公司生产A,B两种机械设备,每台B种设备的成本是A种设备的1.5倍,公司若投入16万元生产A种设备,36万元生产B种设备,则可生产两种设备共10台.请解答下列问题:
(1)A、B两种设备每台的成本分别是多少万元?
(2)若A,B两种设备每台的售价分别是6万元,10万元,公司决定生产两种设备共60台,计划销售后获利不低于126万元,且A种设备至少生产53台,求该公司有几种生产方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地有两条公路,一条是全长600km的普通公路,另一条是全长480km的高速公路,某客车在高速公路上行驶的平均速度比在普通公路上快45![]() /
/![]() ,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需的时间.
,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客车由高速公路从甲地到乙地所需的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
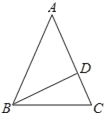
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,则下列结论中①BC=BD=AD;②S△ABD:S△BCD=AD:DC;③BC2=CDAC;④若AB=2,则BC=![]() ﹣1,其中正确的结论的个数是_____个.
﹣1,其中正确的结论的个数是_____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是⊙O 外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.
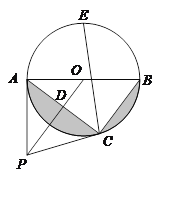
(1)求证:PC是⊙O的切线;
(2)若PD=![]() cm,AC=8cm,求图中阴影部分的面积;
cm,AC=8cm,求图中阴影部分的面积;
(3)在(2)的条件下,若点E是![]() 的中点,连接CE,求CE的长.
的中点,连接CE,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是圆上任意一点,点D是AC中点,OD交AC于点E,BD交AC于点F,若BF=1.25DF,则tan∠ABD的值为( )
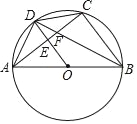
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
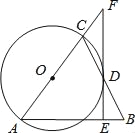
【题目】如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线EF,交AB和AC的延长线于E、F.
(1)求证:FE⊥AB;
(2)当AE=6,sin∠CFD=![]() 时,求EB的长.
时,求EB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为每小时30海里,在此航行过程中,问该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
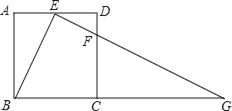
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF:DC=1:4,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为10,求BG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com