
【题目】如图,点P是⊙O 外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.
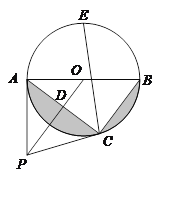
(1)求证:PC是⊙O的切线;
(2)若PD=![]() cm,AC=8cm,求图中阴影部分的面积;
cm,AC=8cm,求图中阴影部分的面积;
(3)在(2)的条件下,若点E是![]() 的中点,连接CE,求CE的长.
的中点,连接CE,求CE的长.
【答案】(1)参见解析;(2)![]() ;(3)
;(3)![]() cm.
cm.
【解析】
(1)连接OC,证明△PAO≌△PCO,得到∠PAO=∠PCO=90 ,证明结论;
(2)证明△ADO∽△PDA,得到成比例线段求出BC的长,根据S阴=S半⊙O-S△ACB求出答案;
(3)连接AE,BE,过点B作BM⊥CE于点M,分别求出CM和EM的长,求和得到答案.
证明: ⑴如图,连接OC,
∵PA切⊙O于A.
∴∠PAO=90.
∵OP∥BC,
∴∠AOP=∠OBC,∠COP=∠OCB.
∵OC=OB,
∴∠OBC=∠OCB,
∴∠AOP=∠COP.
又∵OA=OC,OP=OP,
∴△PAO≌△PCO (SAS).
∴∠PAO=∠PCO=90 ,
又∵OC是⊙O的半径,
∴PC是⊙O的切线.
⑵解法一:
由(1)得PA,PC都为圆的切线,
∴PA=PC,OP平分∠APC,∠ADO=∠PAO=90 ,
∴∠PAD+∠DAO=∠DAO+∠AOD,
∴∠PAD =∠AOD,
∴△ADO∽△PDA.
∴![]() ,
,
∴![]() ,
,
∵AC=8, PD=![]() ,
,
∴AD=![]() AC=4,OD=3,AO=5,
AC=4,OD=3,AO=5,
由题意知OD为△ABC的中位线,
∴BC=2OD=6,AB=10.
∴S阴=S半⊙O-S△ACB=![]() .
.
答:阴影部分的面积为![]() .
.
解法二:

∵AB是⊙O的直径,OP∥BC,
∴∠PDC=∠ACB=90.
∵∠PCO=90 ,
∴∠PCD+∠ACO=∠ACO+∠OCB=90 ,
即∠PCD=∠OCB.
又∵∠OBC =∠OCB,
∴∠PCD=∠OBC,
∴△PDC∽△ACB,
∴![]() .
.
又∵AC=8, PD=![]() ,
,
∴AD=DC=4,PC=![]() .
.
∴![]() ,
,
∴CB=6,AB=10,
∴S阴=S半⊙O-S△ACB=![]() .
.
答:阴影部分的面积为![]() .
.
(3)如图,连接AE,BE,过点B作BM⊥CE于点M.
∴∠CMB=∠EMB=∠AEB=90,
又∵点E是![]() 的中点,
的中点,
∴∠ECB=∠CBM=∠ABE=45,CM=MB =![]() ,BE=ABcos45=
,BE=ABcos45=![]() ,
,
∴ EM=![]() ,
,
∴CE=CM+EM=![]()
![]() .
.
“点睛”本题考查的是切线的判定和性质、扇形面积的计算和相似三角形的判定和性质,灵活运用切线的性质:圆的切线垂直于过切点的半径和切线的判定是解题的关键.


科目:初中数学 来源: 题型:
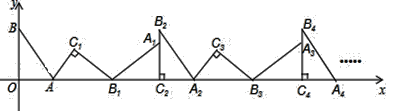
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B,O分别落在点B1,C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(3,0),B(0,4),则点B2018的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
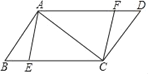
【题目】如图,在平行四边形ABCD中,AB=6,BC=10,对角线AC⊥AB,点E、F分别是BC、AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)当BE长度为 时,四边形AECF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“灵”、“秀”、“黄”、“冈”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,球上的汉字刚好是“黄”的概率为多少?
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图的方法,求出甲取出的两个球上的汉字恰能组成“灵秀”或“黄冈”(汉字不分先后顺序)的概率![]() ;
;
(3)乙从中任取一球,记下汉字后再放回袋中,然后再从中任取一球,记乙取出的两个球上的汉字恰能组成“灵秀”或“黄冈”(汉字不分先后顺序)的概率为![]() ,请直接写出
,请直接写出![]() 的值,并比较
的值,并比较![]() ,
,![]() 的大小.(2+3+2=7)
的大小.(2+3+2=7)
查看答案和解析>>
科目:初中数学 来源: 题型:
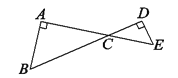
【题目】已知∠A=Rt∠,AB=4,AE=2![]() ,点C在线段AE上运动(不与点A点E重合),过点E作ED⊥BC交BC的延长线于D,则
,点C在线段AE上运动(不与点A点E重合),过点E作ED⊥BC交BC的延长线于D,则![]() 的最大值为( )
的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c经过点(﹣2,0),且对称轴为直线x=1,其部分图象如图所示.对于此抛物线有如下四个结论:
①ac>0;②16a+4b+c=0;③若m>n>0,则x=1+m时的函数值大于x=1﹣n时的函数值;④点(﹣![]() ,0)一定在此抛物线上.其中正确结论的序号是( )
,0)一定在此抛物线上.其中正确结论的序号是( )
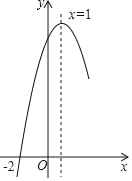
A. ①②B. ②③C. ②④D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是关于
是关于![]() 的方程
的方程![]() 的一个实数根,并且这个方程的两个实数根恰好是等腰三角形
的一个实数根,并且这个方程的两个实数根恰好是等腰三角形![]() 的两条边长,则
的两条边长,则![]() 的周长为( )
的周长为( )
A. 6 B. 8 C. 10 D. 8或10
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com