Question

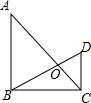
1．将一副三角板按图叠放，∠A=45°，∠D=60°，∠ABC=∠DCB=90°，则△AOB与△DOC的面积之比为3：1．

Answer 1

分析 根据特殊锐角三角函数值可知：$\frac{AB}{DC}=\frac{\sqrt{3}}{1}$，然后可证明△AOB∽△DOC，最后根据相似三角形的面积比等于相似比的平方求解即可．

解答 解：∵∠D=60°，∠DCB=90°，
∴∠DBC=30°．
∴$\frac{DC}{BC}$=$\frac{\sqrt{3}}{3}$．
∵∠A=45°，∠ABC=90°，
∴∠BCA=∠A=45°．
∴AB=BC．
∴$\frac{DC}{AB}=\frac{\sqrt{3}}{3}$．
∵∠ABC=∠DCB=90°，
∴AB∥CD，
∴△AOB∽△DOC．
∴$\frac{{S}_{△AOB}}{{S}_{△DOC}}=（\frac{AB}{CD}）^{2}=3$：1．
故答案为：3：1．

点评 此题考查了相似三角形的判定与性质与三角函数的知识．此题难度不大，解题的关键是数形结合思想的应用与似三角形的面积比等于相似比的平方定理的应用．