
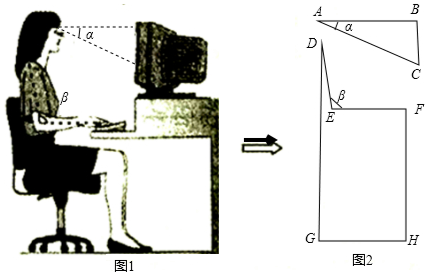
分析 (1)Rt△ABC中利用三角函数即可直接求解;
(2)延长FE交DG于点I,利用三角函数求得∠DEI即可求得β的值,从而作出判断.
解答 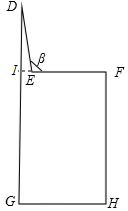 解:(1)∵Rt△ABC中,tanA=$\frac{BC}{AB}$,
解:(1)∵Rt△ABC中,tanA=$\frac{BC}{AB}$,
∴AB=$\frac{BC}{tanA}$=$\frac{BC}{tan20°}$=$\frac{20}{\frac{4}{11}}$=55(cm);
(2)延长FE交DG于点I.
则DI=DG-FH=100-72=28(cm).
在Rt△DEI中,sin∠DEI=$\frac{DI}{DE}$=$\frac{28}{30}$=$\frac{14}{15}$,
∴∠DEI=69°,
∴∠β=180°-69°=111°≠100°,
∴此时β不是符合科学要求的100°.
点评 此题综合性比较强,解此题的关键是把实际问题转化为数学问题,本题只要把实际问题抽象到几何图形中来考虑,就能迎刃而解.


科目:初中数学 来源: 题型:选择题
| A. | 检测某批次灯泡的使用寿命,适宜用全面调查 | |
| B. | 可能性是1%的事件在一次试验中一定不会发生 | |
| C. | 数据3,5,4,1,-2的中位数是4 | |
| D. | “367人中有2人同月同日出生”为必然事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
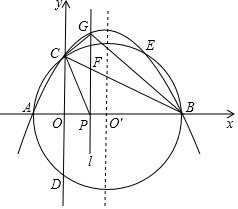 如图,在平面直角坐标系中,已知A(-2,0),C(0,4),点O′为x轴上一点,⊙O′过A,C两点交x轴于另一点B.
如图,在平面直角坐标系中,已知A(-2,0),C(0,4),点O′为x轴上一点,⊙O′过A,C两点交x轴于另一点B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
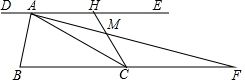 如图,过锐角△ABC的顶点A作DE∥BC,AB恰好平分∠DAC,AF平分∠EAC交BC的延长线于点F.在AF上取点M,使得AM=$\frac{1}{3}$AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是$\frac{1}{12}$,则$\frac{1}{tan∠ACH}$的值是8-$\sqrt{15}$.
如图,过锐角△ABC的顶点A作DE∥BC,AB恰好平分∠DAC,AF平分∠EAC交BC的延长线于点F.在AF上取点M,使得AM=$\frac{1}{3}$AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是$\frac{1}{12}$,则$\frac{1}{tan∠ACH}$的值是8-$\sqrt{15}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com